Definitions of Correlation, Coefficient of Correlation, Correlation Analysis

In this article, we will discuss all definitions of correlation, coefficient of correlation, and correlation analysis.

Correlation:

Correlation is a statistical technique that studies the relationship between two or more variables and correlation analysis involves various methods and techniques used for studying and measuring the extent of the relationship between the two variables.

In other words, the relationship between variables is called correlation. Two variables x and y are said to be correlated if the change in one variable results in a corresponding change in the other variable.

In other words, the two variables x and y are said to be correlated, if these two variables are so related in such a way that a change in the value of one is accompanied either by a direct change or by an inverse change in the values of the other. That is, a decrease in one variable is accompanied by an increase or decrease in the other variable in the correlated variables.

For instance, a relationship exists between the price and demand of a commodity because keeping other things equal, an increase in the price of a commodity shall cause a decrease in the demand for that commodity. The relationship might exist between the heights and weights of the students and between the amount of rainfall in a city and the sales of raincoats in that city.

Hence, correlation is a statistical method for examining relationships between quantitative variables and categorical variables. To put it another way, it’s a measure of how things are related.

Coefficient of Correlation:

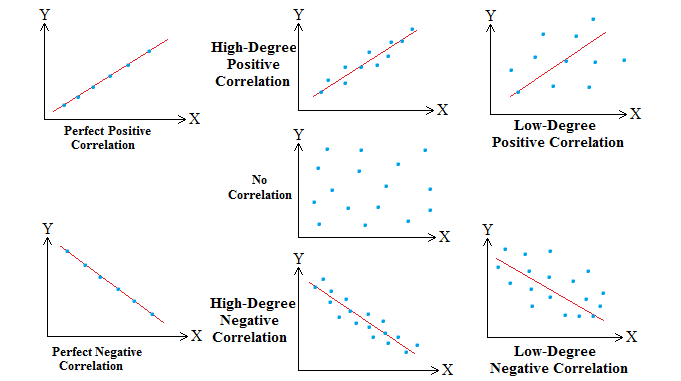
The measure of correlation called the coefficient of correlation (denoted by r) summarizes in one figure the direction and degree of correlation. In other words, the correlation coefficient is a measure of the relationship between two variables. To find the correlation coefficient, divide the covariance of the two variables by the product of their standard deviations. The value of the correlation coefficient is always between -1 and +1.

• The correlation coefficient r has a value of +1 if the two variables have a perfect direct (increasing) linear relationship.
• The correlation coefficient r has a value of -1 if the two variables have a perfect inverse (decreasing) linear relationship.
• The value of the correlation coefficient r is close to 0 if there is little correlation between the two variables.
• In other cases, the value of the correlation coefficient r is between -1 and +1.

Correlation Analysis:

Correlation Analysis is the study of how variables are correlated. As a result, correlation analysis refers to the techniques used to assess the closeness of the relationship between the variables.

These are some of the important definitions of correlation:

♦ Croxton and Cowden say, “When the relationship is of a quantitative nature, the appropriate statistical tool for discovering and measuring the relationship and expressing it in a brief formula is known as correlation”.

♦ A.M. Tuttle says, “Correlation is an analysis of the covariation between two or more variables.”

♦ W.A. Neiswanger says, “Correlation analysis contributes to the understanding of economic behaviour, aids in locating the critically important variables on which others depend, may reveal to the economist the connections by which disturbances spread and suggest to him the paths through which stabilizing forces may become effective.”

♦ L.R. Conner says, “If two or more quantities vary in sympathy so that the movements in one tends to be accompanied by corresponding movements in others then they are said to be correlated.”

(Source – Various books from the college library)

Tags: write all definitions of Correlation, what is the correlation coefficient, explain correlation analysis, correlation coefficient, correlation analysis, definitions of correlation

Copyrighted Material © 2019 - 2024 Prinsli.com - All rights reserved

All content on this website is copyrighted. It is prohibited to copy, publish or distribute the content and images of this website through any website, book, newspaper, software, videos, YouTube Channel or any other medium without written permission. You are not authorized to alter, obscure or remove any proprietary information, copyright or logo from this Website in any way. If any of these rules are violated, it will be strongly protested and legal action will be taken.