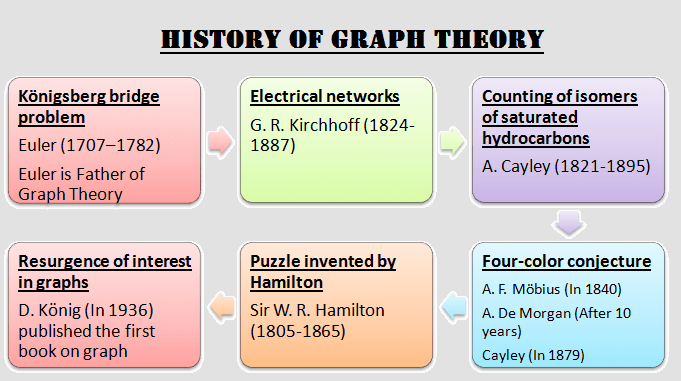
ग्राफ सिद्धांत (Graph Theory) का इतिहास:

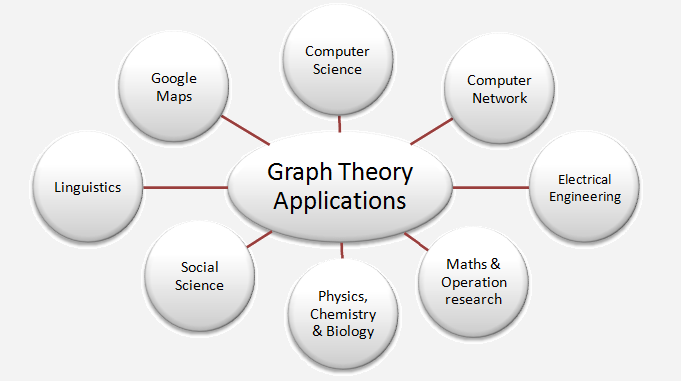
History of Graph Theory in Hindi – ग्राफ सिद्धांत के इतिहास का पता 1735 में लगाया जा सकता है, जब स्विस गणितज्ञ लियोनहार्ड यूलर ने कोनिग्सबर्ग ब्रिज समस्या (Königsberg bridge problem) को हल किया था। ग्राफ का अध्ययन, जिसे ग्राफ सिद्धांत के रूप में भी जाना जाता है, गणित, इंजीनियरिंग, भौतिक, सामाजिक, जैविक और कंप्यूटर विज्ञान, भाषा विज्ञान और कई अन्य विषयों का एक महत्वपूर्ण हिस्सा है। एक ग्राफ का उपयोग असतत वस्तुओं और उनके बीच संबंध से जुड़ी लगभग किसी भी भौतिक स्थिति का प्रतिनिधित्व करने के लिए किया जा सकता है।

एक ग्राफ बिंदुओं का एक संग्रह है जिसे नोड्स या वर्टिसिस (nodes or vertices) के रूप में जाना जाता है जो किनारों (edges) के रूप में ज्ञात लाइनों के नेटवर्क द्वारा एक साथ जुड़े होते हैं। क्योंकि ग्राफ सिद्धांत को अनुप्रयुक्त गणित (applied mathematics) की एक शाखा माना जाता है, इसमें कोई आश्चर्य की बात नहीं है कि ग्राफ सिद्धांत को स्वतंत्र रूप से कई बार खोजा गया है।

ग्राफ सिद्धांत का आविष्कार किसने किया:

1736 में, यूलर (1707-1782) ने एक पेपर प्रकाशित किया जिसमें उन्होंने कोनिग्सबर्ग ब्रिज समस्या (Königsberg bridge problem) को हल किया, जिसने ग्राफ सिद्धांत को जन्म दिया। क्योंकि यह माना जाता है कि ग्राफ सिद्धांत 1736 में कोनिग्सबर्ग ब्रिज समस्या के यूलर के समाधान के प्रकाशन के साथ शुरू हुआ था, यूलर को “ग्राफ थ्योरी के पिता” के रूप में जाना जाने लगा।

अगले 100 वर्षों तक इस क्षेत्र में और कुछ नहीं किया गया।

• फिर, 1847 में, जी आर किरचॉफ (1824-1887) ने अपने अनुप्रयोगों के लिए इलेक्ट्रिक नेटवर्क में tree theory विकसित किया। इलेक्ट्रिक नेटवर्क में किरचॉफ के शोध ने ग्राफ में trees से संबंधित मूलभूत अवधारणाओं और प्रमेयों का विकास किया।

• 10 साल बाद, ए. केली (1821-1895) ने उन trees के बारे में सोचा जो कार्बनिक रासायनिक आइसोमर्स की गिनती से उत्पन्न हुए और संतृप्त हाइड्रोकार्बन CnH2n+2 के आइसोमर्स की गणना करने की कोशिश करते हुए trees की खोज की।

• ग्राफ सिद्धांत में दो अन्य मील के पत्थर किरचॉफ और केली के समय के आसपास स्थापित किए गए थे।
  1. जिसमें से एक, चार रंगों का अनुमान (four-color conjecture) है,
  2. और, दूसरा हैमिल्टन द्वारा आविष्कार की गई एक पहेली है।

• चार रंगों का अनुमान (Four-color conjecture):

Four-color conjecture के अनुसार, किसी भी एटलस (किसी समतल पर एक नक्शा) को रंगने के लिए चार रंग पर्याप्त होते हैं ताकि समान सीमाओं (common borders) वाले देशों में अलग-अलग रंग हों।

पहली बार 1840 में, ए.एफ. मोबियस (1790-1868) ने अपने व्याख्यान में चार-रंग की समस्या (four-color problem) को प्रस्तुत किया था।

करीब 10 साल बाद, ए. डी मॉर्गन (1806-1871) ने लंदन में अपने साथी गणितज्ञों के साथ इस समस्या पर चर्चा की। डी मॉर्गन का पत्र चार-रंग की समस्या का पहला प्रमाणित संदर्भ है।

1879 में, केली ने इस समस्या को “first volume of the Proceedings of the Royal Geographic Society” में प्रकाशित किया, और इसे प्रकाशित करने के बाद यह समस्या अच्छी तरह से ज्ञात हो गई। इसके बाद, प्रसिद्ध चार-रंग अनुमान प्रमुखता में आए और तब से लोकप्रिय बना हुआ है।

आज तक अब भी, चार-रंग का अनुमान (four-color problem) ग्राफ सिद्धांत में अब तक की सबसे प्रसिद्ध अनसुलझी समस्या है, जिसने क्षेत्र में भारी मात्रा में शोध को प्रेरित किया है।

• हैमिल्टन द्वारा आविष्कार की गई पहेली (Puzzle invented by Hamilton):

1859 में, सर डब्ल्यू. आर. हैमिल्टन (1805-1865) ने ग्राफ के लिए एक पहेली (puzzle) दृष्टिकोण का आविष्कार किया और इसे डबलिन में एक गेम निर्माता को 25 गिनी में बेच दिया।

पहेली (puzzle) एक लकड़ी के नियमित डोडेकाहेड्रॉन (एक पॉलीहेड्रॉन, जिसमें 12 faces हैं जिनमें सभी face regular pentagons हैं, और 20 corners और 30 edges हैं। प्रत्येक corner पर 3 edges मिलते हैं ) से बना था। Corners पर 20 महत्वपूर्ण शहरों के नाम अंकित थे। पहेली (puzzle) का लक्ष्य डोडेकाहेड्रॉन के किनारों (edges) के साथ एक मार्ग खोजना था, जो 20 शहरों में से प्रत्येक से ठीक एक बार गुजरता था।

यद्यपि इस विशेष समस्या का समाधान प्राप्त करना सरल है, कोई भी अभी तक किसी भी ग्राफ में इस तरह के पथ (हैमिल्टनियन सर्किट के रूप में जाना जाता है) के अस्तित्व के लिए एक आवश्यक और पर्याप्त स्थिति नहीं खोज सका है।

इस उपयोगी अवधि के बाद, आधी सदी सापेक्ष निष्क्रियता की थी।

• फिर, 1920 के दशक के दौरान, ग्राफ में रुचि का पुनरुत्थान शुरू हुआ। डी. कोनिग इस समयावधि के अग्रदूतों में से एक थे। उन्होंने अन्य गणितज्ञों के साथ-साथ अपने स्वयं के कार्यों को व्यवस्थित किया और 1936 में इस विषय पर पहली पुस्तक प्रकाशित की।

• पिछले 30 वर्षों में ग्राफ सिद्धांत में गहन गतिविधि देखी गई है – शुद्ध और अनुप्रयुक्त (pure and applied) दोनों। इस क्षेत्र में काफी मात्रा में शोध कार्य किया गया है और किया जा रहा है। पिछले एक दशक के दौरान हजारों पत्र प्रकाशित हुए हैं और एक दर्जन से अधिक पुस्तकें लिखी गई हैं।

• इक्कीसवीं सदी में, पहले से ही ग्राफ सिद्धांत की बहुत सारी पुनः खोज हो चुकी हैं।

(Source – Various books from the college library)

Tags: graph theory discrete mathematics in hindi, graph theory history in hindi

Copyrighted Material © 2019 - 2024 Prinsli.com - All rights reserved

All content on this website is copyrighted. It is prohibited to copy, publish or distribute the content and images of this website through any website, book, newspaper, software, videos, YouTube Channel or any other medium without written permission. You are not authorized to alter, obscure or remove any proprietary information, copyright or logo from this Website in any way. If any of these rules are violated, it will be strongly protested and legal action will be taken.