Application of Graph Theory in Real Life in Hindi

Application of Graph Theory in Real Life in Hindi (वास्तविक और दैनिक जीवन में ग्राफ सिद्धांत के अनुप्रयोग) –

ग्राफ सिद्धांत के अनुप्रयोग वास्तविक दैनिक जीवन में भी उपयोगी होते हैं। शायद हम इस बात से अनजान हैं या ध्यान नहीं देते हैं कि हम अपने दैनिक जीवन में ग्राफ थ्योरी का प्रयोग कर रहे हैं। वास्तव में, हमारी दैनिक दिनचर्या की बहुत सारी गतिविधियों में ग्राफ सिद्धांत का उपयोग किया जाता है। ग्राफ रोजमर्रा की जिंदगी में कई वस्तुओं, विचारों, अवधारणाओं, संचालन और प्रक्रियाओं का आधार हैं।

हम जानते हैं कि हमारी दुनिया में सब कुछ आपस में जुड़ा हुआ है; उदाहरण के लिए, शहर सड़क, रेल और हवाई नेटवर्क से जुड़े हुए हैं; इंटरनेट पर पेज हाइपरलिंक से जुड़े होते हैं; एक इलेक्ट्रिक सर्किट या कंप्यूटर चिप के विभिन्न घटक जुड़े हुए हैं, आदि। ग्राफ सिद्धांत उन इंजीनियरों, वैज्ञानिकों और अन्य पेशेवरों की सहायता कर सकता है जो इन नेटवर्कों का विश्लेषण, समझ और अनुकूलन करना चाहते हैं।

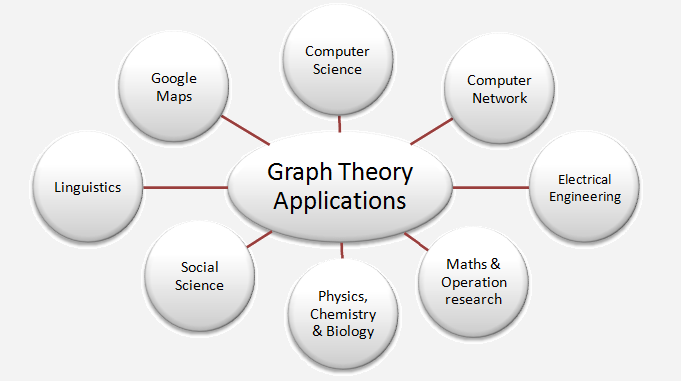
ग्राफ थ्योरी का उपयोग लगभग हर पसंदीदा क्षेत्र में और कई उद्देश्यों के लिए किया जाता है। वास्तविक दुनिया में ग्राफ का उपयोग विभिन्न क्षेत्रों में किया जाता है, जिसमें चिकित्सा, अपराध विज्ञान, इंटरनेट क्षेत्र, गूगल मैप्स / याहू मैप्स, सोशल मीडिया, वेब पेज सर्चिंग, सिटी प्लानिंग, ट्रैफिक कंट्रोल, ट्रांसपोर्टेशन एंड नेविगेशन, ट्रैवलिंग सेल्समैन प्रॉब्लम, मैप कलरिंग, जीएसएम मोबाइल फोन नेटवर्क, टाइम टेबल शेड्यूलिंग आदि शामिल है, और यहां तक ​​​​कि ग्राफ का उपयोग अफवाह फैलाने की एक साधारण सी छोटी स्कूली समस्या के रूप में किया जाता है। ग्राफ सिद्धांत का उपयोग यह निर्धारित करने के लिए भी किया जा सकता है कि वायरस सीमाओं या शहरों में कैसे फैलते हैं। ग्राफ सिद्धांत का उपयोग जीव विज्ञान और चिकित्सा में दवा के लक्ष्यों को अलग करने, प्रोटीन का काम तय करने या अस्पष्ट क्षमता के गुणों को निर्धारित करने के लिए किया जाता है।

तो, आइए दैनिक जीवन में उपयोग किए जाने वाले ग्राफ सिद्धांत के दिलचस्प अनुप्रयोगों पर करीब से नज़र डालें।

1. इंटरनेट के क्षेत्र में ग्राफ सिद्धांत के अनुप्रयोग (Applications of graph theory in the field of the Internet) –

इंटरनेट मानव जाति द्वारा बनाया गया अब तक का दुनिया का सबसे बड़ा नेटवर्क है। इंटरनेट को एक विशाल आभासी ग्राफ माना जाता है।

♦ वेब पेज सर्च में ग्राफ थ्योरी एप्लीकेशन:

Google, Yahoo, और Bing जैसे वेब सर्च इंजनों में वेबसाइट और पेज एक ग्राफ में जुड़े होते हैं, जो वेबसाइटों को रैंक करने में मदद करता है, जिसके कारण Google शीर्ष पर (शुरुआत में) ही सर्वोत्तम परिणाम प्रदर्शित करता है।

वेब सर्च इंजन जैसे Google, Yahoo, Bing, आदि में, यह वेब पेजों की खोज करता है, जहां वेब पेज हाइपरलिंक के माध्यम से इंटरनेट पर एक दूसरे से जुड़े होते हैं। ग्राफ़ में, प्रत्येक vertex एक अलग वेबपेज है, और प्रत्येक edge दो वेब पेजों के बीच एक लिंक (या हाइपरलिंक) है। यह ध्यान रखना महत्वपूर्ण है कि लिंक केवल एक ही दिशा में चलते हैं, इसलिए यह ग्राफ निर्देशित (directed) और बहुत, बहुत, बड़ा है।

एल्गोरिदम, PageRank और Googlebot, का उपयोग कनेक्टिविटी प्रक्रिया में सहायता के लिए किया जाता है। ग्राफ, वेब पेजों और साइटों को जोड़ता है, जो पेजों को रैंक करने में मदद करता है और गूगल को सर्वश्रेष्ठ पेज प्रदर्शित करने में सक्षम बनाता है।

कुछ वेबसाइटों को बड़ी संख्या में इनकमिंग लिंक (incoming links) प्राप्त होते हैं, जबकि कई छोटी वेबसाइटें बहुत कम प्राप्त करती हैं। यह मौलिक अवधारणा है जिसका उपयोग Google खोज परिणामों को क्रमबद्ध (sort) करने के लिए करता है। अधिक इनकमिंग लिंक वाली वेबसाइटें उच्च गुणवत्ता वाली मानी जाती हैं और खोज परिणामों में सबसे ऊपर दिखाई देती हैं। इसलिए, ग्राफ सिद्धांत से एक सरल विचार, पेजरैंक एल्गोरिथम (PageRank Algorithm), ने Google को अन्य सर्च इंजनों की तुलना में बहुत बेहतर बना दिया।

♦ सोशल मीडिया पर दोस्तों को जोड़ने में ग्राफ थ्योरी के अनुप्रयोग:

आइए हम ग्राफ़ के सबसे अच्छे उदाहरणों में से एक पर विचार करें जो रोज़मर्रा की ज़िंदगी में मौजूद है: सोशल मीडिया। सोशल मीडिया में, ग्राफ सिद्धांत की अवधारणा का व्यापक रूप से उपयोग किया जाता है। सोशल मीडिया पर दोस्तों को जोड़ने के लिए ग्राफ थ्योरी एप्लिकेशन का उपयोग किया जाता है। सोशल नेटवर्किंग साइट्स जैसे फेसबुक, व्हाट्सएप, मैसेंजर, ट्विटर, गूगल+, लिंक्डइन आदि में यूजर्स एक बड़े ग्राफ के माध्यम से जुड़े हुए हैं। यहां, लोगों या उपयोगकर्ताओं को Vertices (Nodes) द्वारा दर्शाया जाता है, और Edges उपयोगकर्ताओं के बीच किसी भी संबंध, जैसे कि followers, friendships, likes, या subscriptions को दर्शाते हैं।

वायरल वीडियो के जरिए लोगों से जुड़ने में ग्राफ थ्योरी का इस्तेमाल किया जाता है। इस मामले में प्रत्येक उपयोगकर्ता एक Vertex है, और जब उपयोगकर्ता कनेक्ट होते हैं, तो वे Edges बनाते हैं। जब कोई वीडियो एक निश्चित संख्या में कनेक्शन/दृश्यों तक पहुंचता है, तो इसे वायरल कहा जाता है। ग्राफ थ्योरी सोशल मीडिया पर मजबूत और कमजोर संबंधों को दर्शाता है।

♦ GPS (गूगल मैप्स/याहू मैप्स) का उपयोग करने में ग्राफ सिद्धांत के अनुप्रयोग :

GPS का उपयोग उपयोगकर्ता (User) की प्राथमिकताओं या सेटिंग्स (सबसे तेज़ मार्ग/सबसे छोटा मार्ग) के आधार पर दो स्थानों (गंतव्यों) के बीच मार्ग खोजने के लिए या सबसे सस्ता किराया खोजने के लिए किया जाता है, और GPS का उपयोग करने के लिए ग्राफ़ थ्योरी को लागू किया जाता है। इस मामले में, स्थानों को vertices द्वारा दर्शाया जाता है, और उनके कनेक्शन edges द्वारा दर्शाए जाते हैं जिनमें दूरी या किराया जैसी जानकारी होती है। उपयोगकर्ता सेटिंग्स के आधार पर, सॉफ्टवेयर महत्वपूर्ण पथ (इष्टतम मार्ग) ढूंढता है।

2. यातायात प्रबंधन में ग्राफ सिद्धांत के अनुप्रयोग (Application of graph theory in Traffic Management) –

परिवहन नेटवर्क और यातायात प्रबंधन, वायु और सड़क परिवहन प्रणाली को विकसित करने वाले संचार नेटवर्क के लिए अत्यंत महत्वपूर्ण हैं। ग्राफ थ्योरी परिवहन और नेविगेशन (मार्ग योजना) में भी उपयोगी होते हैं। सभी फ़्लाइट, ट्रेन और सबवे नेटवर्क ग्राफ बनाते हैं, जिनका उपयोग कुशल शेड्यूल बनाते समय किया जा सकता है।

ग्राफ थ्योरी का उपयोग एक इंटेलिजेंट ट्रांसपोर्टेशन सिस्टम (Intelligent Transportation System – ITS) बनाने के लिए किया जाता है। भविष्य में, इंटेलिजेंट ट्रांसपोर्टेशन सिस्टम स्मार्टफोन और सेल्फ-ड्राइविंग कारों से एकत्र किए गए स्थान डेटा (location data) का उपयोग करके कारों को अधिक कुशलता से रूट करके भीड़भाड़ और दुर्घटनाओं को कम करेगा।

इस सिस्टम की मदद से, हम हर साल सड़क पर खोए हुए लाखों घंटे बचा सकते हैं, पर्यावरण प्रदूषण को काफी कम कर सकते हैं, और आपातकालीन सेवाओं को अधिक तेज़ी से यात्रा करने में सक्षम बना सकते हैं।

♦ उड़ान नेटवर्क में ग्राफ सिद्धांत के अनुप्रयोग:

अनगिनत शहरों को सबसे कुशल तरीके से जोड़ने के लिए एयरलाइंस ग्राफ सिद्धांत का उपयोग करती हैं।

• ग्राफ़ थ्योरी का उपयोग करके यातायात के सुरक्षित और व्यवस्थित प्रवाह सुनिश्चित किया जाता है।
• हवाई स्थानों को व्यवस्थित करने और दुर्घटनाओं से बचने के लिए, हवाई यातायात नियंत्रक (Air traffic controllers) ग्राफ थ्योरी का उपयोग करते हैं।
• ग्राफ थ्योरी का उपयोग ट्रैफिक जाम को कम करने के लिए किया जाता है।

♦ सड़क नेटवर्क में ग्राफ सिद्धांत के अनुप्रयोग:

ग्राफ थ्योरी का उपयोग एक संपूर्ण सड़क परिवहन प्रणाली (perfect road transportation system) के साथ-साथ एक इंटेलिजेंट ट्रांसपोर्टेशन सिस्टम (intelligent transportation system) बनाने के लिए किया जाता है। सभी सड़कें और राजमार्ग भी एक बड़े नेटवर्क का निर्माण करते हैं जिसका उपयोग नेविगेशन सेवाएं (जैसे Google मानचित्र) दो स्थानों के बीच सबसे छोटा मार्ग खोजने के लिए करती हैं।

• ग्राफ थ्योरी का उपयोग तेज गति से यात्रा करने के लिए किया जाता है।
• ग्राफ थ्योरी का उपयोग ट्रैफिक जाम को कम करने के लिए किया जाता है।
• ग्राफ थ्योरी का उपयोग वाहन दुर्घटनाओं को रोकने के लिए किया जाता है।

3. ट्रैफिक लाइट में ग्राफ सिद्धांत के अनुप्रयोग (Application of graph theory in Traffic Lights) –

ग्राफ थ्योरी का उपयोग ट्रैफिक लाइटों के संचालन में किया जाता है, विशेष रूप से हरे/लाल को बदलने और उनके बीच के समय में।

यहां, हम आवश्यक चक्रों (cycles) की संख्या के लिए, रंगीन संख्या की पहचान करके, समय और स्थान के संघर्षों (time and space conflicts) को हल करने के लिए, वर्टेक्स कलरिंग तकनीक (Vertex Coloring Technique) का उपयोग करते हैं।

4. अपराधों को सुलझाने में ग्राफ सिद्धांत के अनुप्रयोग (Application of graph theory in solving Crimes) –

वास्तविक दुनिया में, यह ग्राफ सिद्धांत का सबसे महत्वपूर्ण अनुप्रयोग है। ग्राफ सिद्धांत, जैसा कि आप जानते होंगे, लिंकिंग और लिंकिंग के विश्लेषण के बारे में है। यह आपको एक गंभीर अपराध के मास्टरमाइंड के लिए झूठी अफवाह फैलाने वाले को खोजने में मदद कर सकता है।

ग्राफ विधियों को आपराधिक विश्लेषण प्रणालियों (criminal investigation systems) के लिए लागू किया जा सकता है। इस मामले में, यह माना जाता है कि जांच के लोग (घटनाएं) एक ग्राफ के vertices द्वारा दर्शाए जाते हैं, और edges संभावित कनेक्शन का प्रतिनिधित्व करते हैं।

5. रोड ब्लॉकेज को दूर करने के लिए ग्राफ थ्योरी के अनुप्रयोग (Application of graph theory to clear Road Blockage) –

जब किसी शहर की सड़कें बर्फ के कारण अवरुद्ध हो जाती हैं, तो शहर सड़कों पर नमक डालने की योजना बनाता है। लेकिन सड़कों पर नमक डालने के लिए पहले से प्लानिंग करनी पड़ती है।

इस स्थिति में, हम सबसे कुशल तरीके से सड़कों को पार करने (traverse) के लिए यूलर पथ या सर्किट (Euler paths or circuits) का उपयोग करते हैं।

6. मार्ग विकसित करने के लिए ग्राफ सिद्धांत के अनुप्रयोग (Application of graph theory to Develop Routes) –

ग्राफ थ्योरी की मदद से, एक स्कूल प्रशासन छात्रों को लेने और उन्हें स्कूल पहुंचाने के लिए बस मार्ग (bus routes) विकसित करने की योजना बना रहा है। प्रत्येक स्टॉप को एक vertex द्वारा दर्शाया जाता है, और मार्ग को एक edge द्वारा दर्शाया जाता है। इस मामले में, हम मार्ग में प्रत्येक vertex को शामिल करने की दक्षता का प्रतिनिधित्व करने के लिए हैमिल्टनियन पथ (Hamiltonian path) का उपयोग करते हैं।

ग्राफ थ्योरी की मदद से, वाटर पार्क, थीम पार्क, या चिड़ियाघर घूमते समय, आप विशिष्ट आकर्षण या सभी आकर्षण देखने के लिए एक कुशल मार्ग की योजना बना सकते हैं। ग्राफ में प्रत्येक शीर्ष को हैमिल्टन के पथ या परिपथ (Hamiltonian path) द्वारा दर्शाया जाता है।

7. GSM मोबाइल फोन नेटवर्क और मैप कलरिंग में ग्राफ थ्योरी के अनुप्रयोग (Application of graph theory in GSM Mobile Phone Networks and Map Coloring) –

सभी मोबाइल आस-पास में सेल खोज कर जीएसएम नेटवर्क से जुड़ते हैं। किसी भी जीएसएम मोबाइल फोन नेटवर्क के लिए, वर्टेक्स कलरिंग एल्गोरिथम (vertex colouring algorithm) का उपयोग अधिकतम चार अलग-अलग आवृत्तियों (frequencies) पर आवंटित करने के लिए किया जा सकता है।

GSM संचालित करने के लिए केवल चार आवृत्ति रेंज पर्याप्त हैं, क्योंकि वर्टेक्स कलरिंग एल्गोरिथम के अनुसार, केवल चार अलग-अलग रंगों का उपयोग करके सेलुलर क्षेत्रों के मानचित्र को ठीक से रंगा जा सकता है।

ग्राफ सिद्धांत के अन्य अनुप्रयोग इस प्रकार हैं (Other application of graph theory in real life):

• 8. एकीकृत परिपथों (Integrated circuits) में शामिल लाखों ट्रांजिस्टर को जोड़ने के लिए कंप्यूटर चिप्स को डिजाइन करने के लिए ग्राफ सिद्धांत का उपयोग किया जाता है।

• 9. कंप्यूटर नेटवर्क सुरक्षा में भी ग्राफ सिद्धांत का उपयोग किया जाता है।

• 10. कंप्यूटर हार्डवेयर में, भौतिक परत की सीमाओं (physical layer’s limitations) को मॉडल करने के लिए ग्राफ सिद्धांत अवधारणाओं का उपयोग किया जाता है।

• 11. डेटा माइनिंग में ग्राफ थ्योरी का मुख्य अनुप्रयोग क्षेत्र ग्राफ माइनिंग है। डेटा के संबंधपरक पहलू (relational aspect) को ग्राफ माइनिंग द्वारा दर्शाया जाता है।

• 12. हम शेड्यूलिंग, जैसे जॉब शेड्यूलिंग, एयरक्राफ्ट शेड्यूलिंग, आदि में ग्राफ थ्योरी की ग्राफ कलरिंग तकनीकों (Graph coloring techniques) का उपयोग करते हैं।

Read Also: Application of Graph Theory in Various Fields in Hindi

(Source – Various books from the college library)

Read this article in ‘English’

ग्राफ सिद्धांत के कई अन्य अनुप्रयोग हो सकते हैं जिन्हें हो सकता है कि हम इस लेख में भूल गए हों, यदि आप हमें इस विषय के बारे में और बताना चाहते हैं, तो Please Comment.

Copyrighted Material © 2019 - 2024 Prinsli.com - All rights reserved

All content on this website is copyrighted. It is prohibited to copy, publish or distribute the content and images of this website through any website, book, newspaper, software, videos, YouTube Channel or any other medium without written permission. You are not authorized to alter, obscure or remove any proprietary information, copyright or logo from this Website in any way. If any of these rules are violated, it will be strongly protested and legal action will be taken.