Basic Concept of Trigonometry: Measurement of Angles

Introduction of Trigonometry:

Trigonometry is the branch of mathematics that deals with the measurement of a triangle’s parts, sides, and angles. Trigonometry is based on certain ratios known as trigonometric functions. The trigonometric functions were first used in surveying, navigation, and engineering. These functions are also important in the study of all kinds of vibratory phenomena—sound, light, electricity, and so on. As a result, a significant portion of the subject is devoted to investigating the properties and relationships of trigonometric functions.

Definition of a Ray: What is the ray?

To properly define an angle, we must first define a ray. A ray is a segment of a line that is directed in one direction, that is, a ray is a directed line segment.

A ray is made up of one fixed point on a line and all points that extend in one direction (or same direction) from that point. The first point is referred to as the ray’s endpoint.

To refer to a specific ray, we specify its endpoint and any other point on it. The ray shown in the following figure can be denoted by Ray AB, or in symbol form $\overrightarrow {AB}$ .

Definition of Angle: What is the angle?

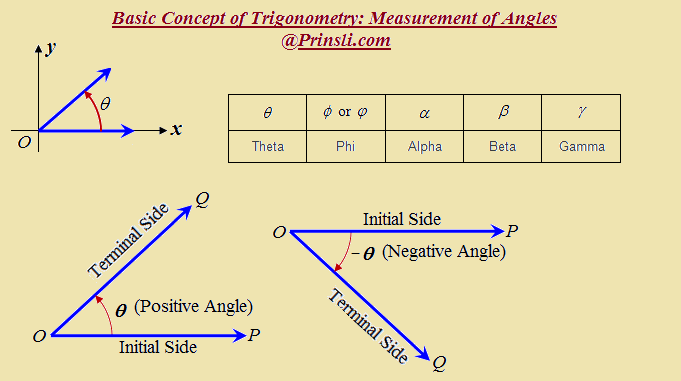
An angle is formed by two rays (half-lines), where the common endpoint of these two rays is called the vertex and the half-lines are called the sides of the angle.

In the following Figure, the Angle POQ is formed by the two Rays OP and OQ. Point O is called the vertex, and the rays (half-lines): OP and OQ; are called the sides of the Angle POQ.

Angles can be named using a point on each ray and the vertex, for example, the angle shown in the above figure can be denoted by Angle POQ, or in symbol form ∠POQ or ∠O, in which the middle letter always represents the vertex of the angle (in this case, O is the given angle).

In other words, an angle is thought of as being generated by revolving a ray in a plane from the initial position OP to a terminal position OQ. Then O is again the vertex, OP is called the initial side, and OQ is called the terminal side of the angle.

Measurement of an Angle:

The amount of rotation from the initial side to the terminal side of an angle is called the measurement of the angle.

Greek letters are usually used as variables in angle measurement. The Greek letters commonly used to represent angles are listed below.

Sense of an Angle:

If the initial side of an angle rotates counterclockwise or anti-clockwise direction to get to the terminal side, then the sense of the angle is called positive. In other words, an angle is called positive if the rotational direction (shown by a red curved arrow in the figure) is counterclockwise or anti-clockwise.

If the initial side of an angle rotates clockwise direction to get to the terminal side, then the sense of the angle is called negative. In other words, an angle is called negative if the rotational direction (shown by a red curved arrow in the figure) is clockwise.

That is, if we measure an angle in a counterclockwise direction the measurement is positive and if we measure in a clockwise direction the measurement is negative.

Definition of Angle in Maths by RD Sharma:

Consider a ray OA. If this ray rotates about its endpoint O and takes the position OB, then we say that the Angle AOB has been generated.
“Thus, an angle is considered as the figure obtained by rotating a given ray about its end-point.“

The revolving ray is called the generating line of the angle. the initial position OA is called the initial side and the final position OB is called the terminal side of the angle. The endpoint O about which the ray rotates is called the vertex of the angle.

Measure of an Angle:

The measure of an angle is the amount of rotation from the initial side to the terminal side.

Angles in a Unit Circle:

In a unit circle, angles start on the x-axis and are measured counterclockwise about the origin.

Standard Position of an Angle:

In a unit circle, if the vertex of the angle is located at the origin and one ray is on the positive x-axis, then the angle is in the standard position, as shown in the above figure. The ray on the x-axis is known as the initial side while the other ray is known as the terminal side.

Quadrantal Angle:

A quadrantal angle is one in which the terminal side of an angle is “on” the axes (for example, angles 0°, 90°, 180°, 270°, and 360° are the quadrantal angles).

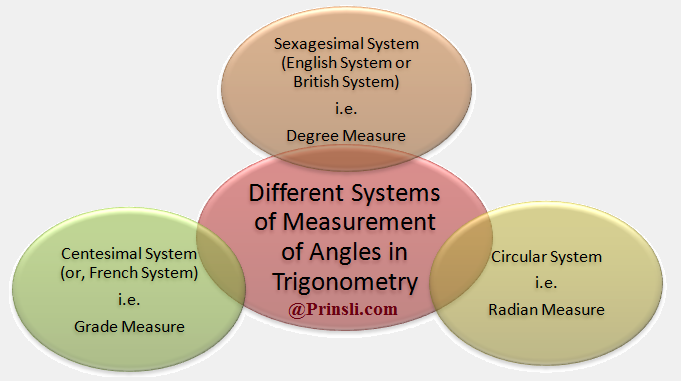
Measurement of an Angle:

Angles are measured in the terms of degree (°), radians (rad) or gradians (grad or g).

There are 360 degrees or 2π radians or 400 gradians in a complete rotation.

♦ Degree –

The degree is a measure of angles and it is denoted by the symbol °. There are 360 degrees in a full rotation, so a degree (°) is the measure of the central angle subtended by an arc of a circle equal to 1/360 of the circumference of the circle.

In addition, a minute (‘) is 1/60 of a degree; and a second (“) is 1/60 of a minute or 1/3600 of a degree. Hence,

1 Degree = 60 Minutes, that is, 1°=60′,

and,

1 Minute = 60 Seconds, that is, 1′ = 60”.

And so,

1 Degree = 3600 Seconds, that is, 1°= 3600”.

Types of Angles:

Generally, an angle is measured in degrees by using a protractor. The types of angles are classified according to their degree values. There are majorly six types of angles. The types of angles with their properties are as follows:

1. Acute Angle: It lies between 0° to 90°, that is, 0°< θ <90°.

2. Right Angle: The angle which is exactly equal to 90°, that is, θ=90°.

3. Obtuse Angle: It lies between 90° to 180°, that is, 90°< θ <180°.

4. Straight Angle: The angle which is exactly equal to 180°, that is, θ=180°.

5. Reflex Angle: It lies between 180° and 360°, that is, 180°< θ <360°.

6. Full Rotation: The complete rotation of angle equal to 360°, that is, the angle which is exactly equal to 360°, that is, θ=360°.

♦ Radian –

A radian (rad) is the measure of the central angle subtended by an arc of a circle equal to the circle’s radius.

Hence, a radian is also a measure of angles, so we can also represent angles in radians, i.e., in terms of pi (π). Where,

360° = 2π in radians

Because a full rotation equals 2π radians, one degree is equivalent to π/180 radians. That is,

1°= π/180 radians = 0.017453 rad.

And,

1 radian = 180°/π = 57.296° = 57°17’45”,

where, π=3.14159.

♦ Gradian –

The gradian is also a measure of angles and it is denoted by the symbol g, so we can also represent angles in gradians, where,

1 Gradian = 0.90 Degree, that is, 1 grad = 0.9°.

Because there are 400 gradians in a full rotation, a gradian is the measure of the central angle subtended by an arc of a circle equal to 1/400 of the circumference of the circle.

In other words, a gradian is equal to 1/400 of a circle or a revolution or 9/10° or 0.9°. The grad is defined more precisely as π/200 radians.

Because 90° equals 100 gradians, this unit simplifies right angle measurements.

Hence, finally, we can say that,

1 degree = π/180 radians = 10/9 gradians,
1 radian = 180/π degrees = 200/π gradians,
1 gradian = 0.9 degrees = π/200 radians.

And, also,

A Right Angle = 90° = π/2 rad = 100 grad,

A Straight Angle = 180° = π rad = 200 grad,

A Full Rotation = 360° = 2π rad = 400 grad.

Acute Angle: ${0^ \circ } < \theta < {90^ \circ }$ , or $0 < \theta < \frac{\pi }{2}$ , or $0\,{\rm{g}} < \theta < 100\,{\rm{g}}$

Obtuse Angle: ${90^ \circ } < \theta < {180^ \circ }$ , or $\frac{\pi }{2} < \theta < \pi$ , or $100\,{\rm{g}} < \theta < 200\,{\rm{g}}$

Reflex Angle: ${180^ \circ } < \theta < {360^ \circ }$ , or $\pi < \theta < 2\pi$ , or $200\,{\rm{g}} < \theta < 400\,{\rm{g}}$

Tags: key terminology of trigonometry with measurement of angle, measurement of angles in trigonometry

All content on this website is copyrighted. It is prohibited to copy, publish or distribute the content and images of this website through any website, book, newspaper, software, videos, YouTube Channel or any other medium without written permission. You are not authorized to alter, obscure or remove any proprietary information, copyright or logo from this Website in any way. If any of these rules are violated, it will be strongly protested and legal action will be taken.