trigonometrical functions of angles of any size and sign, Basic Trigonometry All Formulas, Trigonometric Ratios, Trigonometry formulas for class 10, Trigonometry formulas for class 11, Trigonometry formulas for class 12

Introduction of Basic Trigonometry Formulas – We know that trigonometry is the branch of mathematics that deals with the measurement of a triangle’s parts, sides, and angles. Hence, trigonometry is also defined as the study of relationships between triangle side lengths and angles. Trigonometry is based on certain ratios known as trigonometric functions. These trigonometric functions are used in surveying, navigation, engineering, etc.

Trigonometry and its formulae have a plethora of uses. For example, in Geography, triangulation is used to measure the distance between landmarks; in Astronomy, triangulation is used to measure the distance to nearby stars and in satellite navigation systems also. Trigonometry formulas can be used to solve many different types of problems. These problems may include trigonometric ratios (sin, cos, tan, cot, sec, cosec), Pythagorean identities, etc.

All basic formulas of trigonometry, such as co-function identities (shifting angles), sum and difference identities, double angle identities, half-angle identities etc. are given here. Students in Classes 10, 11, and 12 will benefit from learning and memorising these trigonometry math formulas in order to get success in this topic.

The Principal Formulae In Trigonometry:

We only consider right-angled triangles when learning about trigonometric formulas. A Right-Angled Triangle has three sides: the Hypotenuse, the opposite side (Perpendicular), and the adjacent side (Base). The hypotenuse is the longest side, the perpendicular is the side opposite the angle, and the adjacent side is the side adjacent to the angle i.e. the side on which both the hypotenuse and the opposite side rest.

Generally, a hypotenuse is denoted by the symbol H, perpendicular is denoted by the symbol P, and base is denoted by the symbol B.

♦ Formulas In Trigonometry Related to Circle and Angles:

1. Area of a Circle is, $A = \pi {r^2}$

2. Circumference of a circle is, $C = 2\pi r$

where, $\pi = 3.14159...$ [Approximation values of π are $\frac{{22}}{7}$ and $\frac{{355}}{{113}}$ ]

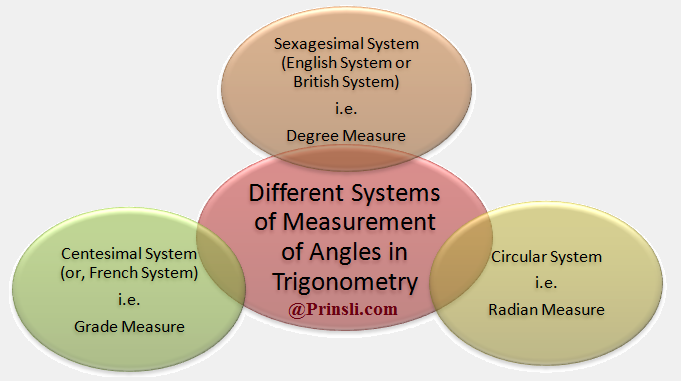
3. 1 Radian = 57.296° = 57°17’44.8” approximately.

4. 1 Right Angle = 90° = π/2 radians = 100^g.

5. 2 Right Angles = 180° = π radians = 200^g.

6. In a circle, ${\rm{Angle}} = \frac{{{\rm{arc}}}}{{{\rm{radius}}}} \times {\rm{Radian}}$

7. Pythagorean Theorem: In any right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. That is,

(Hypotenuse)² = (Perpendicular)² + (Base)²

♦ Basic Trigonometric Function Formulas:

Trigonometric Ratio: Finding the remaining sides and angles of a triangle when some of its sides and angles are given is the most important task of trigonometry. To solve this problem, we use some ratios of the sides of a triangle with respect to its acute angle. These ratios of acute angles are known as Trigonometric Ratios of angles.

The ratio of the lengths of two sides of a right triangle is called a trigonometric ratio.

When the things cannot be measured directly, then trigonometric ratios are used to find the measurement indirectly. Trigonometric ratios help to measure the height or length of an object or the distance between two different objects.

There are basically 6 ratios used in Trigonometry. They are called trigonometric functions. The six trigonometric functions are sine (sin), cosine (cos), tangent (tan), cotangent (cot), secant (sec), and cosecant (cosec or csc).

The Right Triangle Definition: For an acute angle θ in a right triangle:

1. $\sin \theta = \frac{{{\rm{Perpendicular}}}}{{{\rm{Hypotenuse}}}} = \frac{P}{H}$

2. $\cos \theta = \frac{{{\rm{Base}}}}{{{\rm{Hypotenuse}}}} = \frac{B}{H}$

3. $\tan \theta = \frac{{{\rm{Perpendicular}}}}{{{\rm{Base}}}} = \frac{P}{B}$

4. $\cot \theta = \frac{{{\rm{Base}}}}{{{\rm{Perpendicular}}}} = \frac{B}{P}$

5. $\sec \theta = \frac{{{\rm{Hypotenuse}}}}{{{\rm{Base}}}} = \frac{H}{B}$

6. $\csc \theta = \frac{{{\rm{Hypotenuse}}}}{{{\rm{Perpendicular}}}} = \frac{H}{P}$

♦ Reciprocal Identities:

The Reciprocal Identities for trigonometric functions are as follows:

1. $\sin \theta = \frac{1}{{\csc \theta }}$ , and $\csc \theta = \frac{1}{{\sin \theta }}$

2. $\cos \theta = \frac{1}{{\sec \theta }}$ , and $\sec \theta = \frac{1}{{\cos \theta }}$

3. $\tan \theta = \frac{1}{{\cot \theta }}$ , and $\cot \theta = \frac{1}{{\tan \theta }}$

♦ Quotient Identities:

The Quotient Identities for trigonometric functions are as follows:

1. $\tan \theta = \frac{{\sin \theta }}{{\cos \theta }}$

2. $\cot \theta = \frac{{\cos \theta }}{{\sin \theta }}$

♦ Pythagorean Identities in Trigonometry:

The Pythagorean identities in trigonometry are as follows:

1. ${\sin ^2}\theta + {\cos ^2}\theta = 1$ , that is,

${\sin ^2}\theta = 1 - {\cos ^2}\theta$ , and

${\cos ^2}\theta = 1 - {\sin ^2}\theta$

2. $1 + {\tan ^2}\theta = {\sec ^2}\theta$ , that is,

${\sec ^2}\theta - {\tan ^2}\theta = 1$ , and

${\sec ^2}\theta - 1 = {\tan ^2}\theta$

3. $1 + {\cot ^2}\theta = {{\mathop{\rm cosec}\nolimits} ^2}\theta$ , that is,

${{\mathop{\rm cosec}\nolimits} ^2}\theta - {\cot ^2}\theta = 1$ , and

${{\mathop{\rm cosec}\nolimits} ^2}\theta - 1 = {\cot ^2}\theta$

Important Note:

1. It is important to note that “sin θ” stands for “sine of angle θ,” not multiplication of sin and θ. The same is true for other trigonometric ratios.

2. The trigonometric ratios listed above are defined for an acute angle θ.

3. The above trigonometric ratios depend only on the value of angle θ.

4. The trigonometric ratios listed above are the same for the same angle.

♦ Trigonometric Ratios for Unit Circle:

Trigonometric Ratios for a unit circle, where the radius is 1 and the angle θ are defined as follows:

1. $\sin \theta = \frac{P}{H} = \frac{y}{1} = y$

2. $\cos \theta = \frac{B}{H} = \frac{x}{1} = x$

3. $\tan \theta = \frac{P}{B} = \frac{y}{x}$

4. $\cot \theta = \frac{B}{P} = \frac{x}{y}$

5. $\sec \theta = \frac{H}{B} = \frac{1}{x}$

6. $\csc \theta = \frac{H}{P} = \frac{1}{y}$

♦ Trigonometry Table Formula:

The following table contains trigonometry formulas for angles that are popularly used in solving problems.

Hence, From this trigonometry table, it is obvious that,

$\sin {0^ \circ } = 0$ ; $\cos {0^ \circ } = 1$ ; $\tan {0^ \circ } = 0$

$\cot {0^ \circ } = \infty$ ; $\sec {0^ \circ } = 1$ ; $\csc {0^ \circ } = \infty$

$\sin {90^ \circ } = 1$ ; $\cos {90^ \circ } = 0$ ; $\tan {90^ \circ } = \infty$

$\cot {90^ \circ } = 0$ ; $\sec {90^ \circ } = \infty$ ; $\csc {90^ \circ } = 1$

$\sin {30^ \circ } = \cos {60^ \circ } = \frac{1}{2}$

$\sin {60^ \circ } = \cos {30^ \circ } = \frac{{\sqrt 3 }}{2}$

$\sin {45^ \circ } = \cos {45^ \circ } = \frac{1}{{\sqrt 2 }}$

$\tan {30^ \circ } = \cot {60^ \circ } = \frac{1}{{\sqrt 3 }}$

$\tan {60^ \circ } = \cot {30^ \circ } = \sqrt 3$

$\tan {45^ \circ } = \cot {45^ \circ } = 1$

$\sec {30^ \circ } = \csc {60^ \circ } = \frac{2}{{\sqrt 3 }}$

$\sec {60^ \circ } = \csc {30^ \circ } = 2$

$\sec {45^ \circ } = \csc {45^ \circ } = \sqrt 2$

Also,

$\sin {15^ \circ } = \cos {75^ \circ } = \frac{{\sqrt 3 - 1}}{{2\sqrt 2 }}$

$\sin {75^ \circ } = \cos {15^ \circ } = \frac{{\sqrt 3 + 1}}{{2\sqrt 2 }}$

$\sin {18^ \circ } = \cos {72^ \circ } = \frac{{\sqrt 5 - 1}}{4}$

$\sin {54^ \circ } = \cos {36^ \circ } = \frac{{\sqrt 5 + 1}}{4}$

♦ Trigonometrical Functions of Angles of any size and sign:

Even and Odd Angle Formulas in Trigonometry:

Even and Odd Angle Formulas in Trigonometry are as follows:

$\sin \left( { - \theta } \right) = - \sin \theta$

$\cos \left( { - \theta } \right) = \cos \theta$

$\tan \left( { - \theta } \right) = - \tan \theta$

$\cot \left( { - \theta } \right) = - \cot \theta$

$\sec \left( { - \theta } \right) = \sec \theta$

$\csc \left( { - \theta } \right) = - \csc \theta$

Hence it is obvious that cosine (cos) and secant (sec) functions are Even functions, while sine (sin), tangent (tan), cotangent (cot), and cosecant (cosec or csc) are Odd functions.

Cofunction Identities or Cofunction Formulas of Trigonometry:

In trigonometry, Cofunction Identities or Cofunction Formulas describe the relationship between various trigonometric functions and their complementary angles. The 6 Cofunction Identities are as follows:

$\sin \left( {{{90}^ \circ } - \theta } \right) = \cos \theta$

$\cos \left( {{{90}^ \circ } - \theta } \right) = \sin \theta$

$\tan \left( {{{90}^ \circ } - \theta } \right) = \cot \theta$

$\cot \left( {{{90}^ \circ } - \theta } \right) = \tan \theta$

$\sec \left( {{{90}^ \circ } - \theta } \right) = \csc \theta$

$\csc \left( {{{90}^ \circ } - \theta } \right) = \sec \theta$

Trigonometrical ratios of Angle (90°+θ) in terms of those of θ, for all values of θ:

In trigonometry, trigonometrical ratios of Angle (90°+θ) in terms of those of θ, for all values of θ are as follows:

$\sin \left( {{{90}^ \circ } + \theta } \right) = \cos \theta$

$\cos \left( {{{90}^ \circ } + \theta } \right) = - \sin \theta$

$\tan \left( {{{90}^ \circ } + \theta } \right) = - \cot \theta$

$\cot \left( {{{90}^ \circ } + \theta } \right) = - \tan \theta$

$\sec \left( {{{90}^ \circ } + \theta } \right) = - \csc \theta$

$\csc \left( {{{90}^ \circ } + \theta } \right) = \sec \theta$

Trigonometrical ratios of Angle (180°-θ) in terms of those of θ, for all values of θ, or, Supplementary Angles:

We know that two angles are supplementary if their sum is equal to two right angles, that is, 180°. Hence, the supplement of any angle θ will be 180°-θ. In trigonometry, trigonometrical ratios of Angle (180°-θ) in terms of those of θ, for all values of θ are as follows:

$\sin \left( {{{180}^ \circ } - \theta } \right) = \sin \theta$

$\cos \left( {{{180}^ \circ } - \theta } \right) = - \cos \theta$

$\tan \left( {{{180}^ \circ } - \theta } \right) = - \tan \theta$

$\cot \left( {{{180}^ \circ } - \theta } \right) = - \cot \theta$

$\sec \left( {{{180}^ \circ } - \theta } \right) = - \sec \theta$

$\csc \left( {{{180}^ \circ } - \theta } \right) = \csc \theta$

Trigonometrical ratios of Angle (180°+θ) in terms of those of θ, for all values of θ:

In trigonometry, trigonometrical ratios of Angle (180°+θ) in terms of those of θ, for all values of θ are as follows:

$\sin \left( {{{180}^ \circ } + \theta } \right) = - \sin \theta$

$\cos \left( {{{180}^ \circ } + \theta } \right) = - \cos \theta$

$\tan \left( {{{180}^ \circ } + \theta } \right) = \tan \theta$

$\cot \left( {{{180}^ \circ } + \theta } \right) = \cot \theta$

$\sec \left( {{{180}^ \circ } + \theta } \right) = - \sec \theta$

$\csc \left( {{{180}^ \circ } + \theta } \right) = - \csc \theta$

Trigonometrical ratios of Angle (360°+θ) in terms of those of θ, for all values of θ:

In trigonometry, trigonometrical ratios for an Angle (360°+θ) are the same as those for θ, for all values of θ. These formulas are as follows:

$\sin \left( {{{360}^ \circ } + \theta } \right) = \sin \theta$

$\cos \left( {{{360}^ \circ } + \theta } \right) = \cos \theta$

$\tan \left( {{{360}^ \circ } + \theta } \right) = \tan \theta$

$\cot \left( {{{360}^ \circ } + \theta } \right) = \cot \theta$

$\sec \left( {{{360}^ \circ } + \theta } \right) = \sec \theta$

$\csc \left( {{{360}^ \circ } + \theta } \right) = \csc \theta$

In the next article, we will learn all basic Trigonometric Identities and formulas: such as Sum and Difference identities, Double Angle identities, Half-Angle identities, Thrice of Angle Formulas, Product to Sum formulas, Sum to Product formulas etc.

Tags: trigonometry formula, trigonometry formulas for class 10, trigonometry all formula, trigonometry formulas for class 11, trigonometry table formula, trigonometry formulas for class 12, basic trigonometry formulas, Co function Identities or Co function Formulas, Pythagorean trigonometric identity

All content on this website is copyrighted. It is prohibited to copy, publish or distribute the content and images of this website through any website, book, newspaper, software, videos, YouTube Channel or any other medium without written permission. You are not authorized to alter, obscure or remove any proprietary information, copyright or logo from this Website in any way. If any of these rules are violated, it will be strongly protested and legal action will be taken.