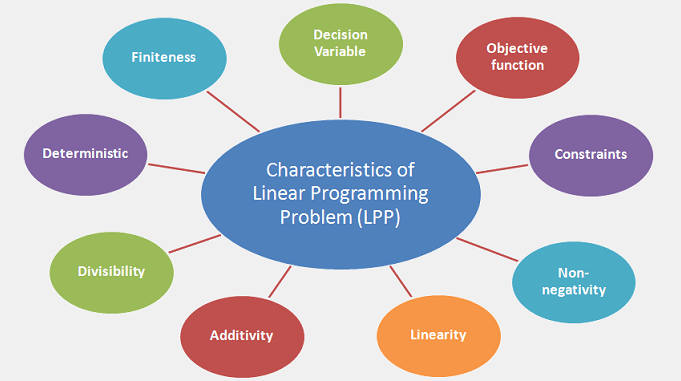
Characteristics of Linear Programming Problem (LPP):
The characteristics of a linear programming problem (LPP) are as follows: (1) decision variables (2) objective function (3) constraints (4) Non-negativity (5) Linearity (6) Additivity (7) Divisibility (8) Deterministic (Certainty) (9) Finiteness. These characteristics are defined below –
(1) Decision Variable:
The decision variables are represented by x, y, etc, and they refer to limited resources.
(2) Objective function:
The objective function is the linear function between decision variables, that is to be maximized or minimized. In most business situations, the objective is to maximize profit or minimize costs.
(3) Constraints:
The restrictions or limits which are determined to make the solution optimum are called constraints.
(4) Non-negativity:
Variables must have a value of zero or positive and not negative. In the case of production, for example, the management can decide on any particular product number in positive or minimal zero, not negative.
(5) Linearity:
The relationships between variables must be linear. The term “linear” refers to a proportionate relationship between two or more variables, with the degree of variables being a maximum one.
(6) Additivity:
It means that the total of all activities is the sum of each individual activity. In other words, none of the activities interacts with one another. For example, if a machine takes t hours to make the first item and s hours to make the second item, then the total time to make both items will be t+s, provided the time taken to change the machine from the first item to the second item is negligible.
(7) Divisibility:
Decision variables can have fractional values.
(8) Deterministic (Certainty):
In the linear programming models, all the parameters are assumed to be known exactly.
(9) Finiteness:
There are a finite number of decision variables and constraints.
Properties of linear programming model:
The following properties must be present in any linear programming model (problem):
(a) There must be a linear relationship between variables and constraints.
(b) The linear programming model should have an objective function.
(c) There must be structural constraints in the linear programming model.
(d) Non-negativity constraints must be present in the linear programming model.
Assumptions in Linear Programming Problem (LPP):
The assumptions of linear programming problem (LPP) are as follows:
(1) Proportionality:
The decision variables are represented by x, y, etc, and they refer to limited resources.
(2) Additivity:
It means that the total of all activities is the sum of each individual activity. In other words, none of the activities interacts with one another. For example, if a machine takes t hours to make the first item and s hours to make the second item, then the total time to make both items will be t+s, provided the time taken to change the machine from the first item to the second item is negligible.
(3) Multiplicativity:
The objective function is the linear function between decision variables, that is to be maximized or minimized. In most business situations, the objective is to maximize profit or minimize costs.
(4) Divisibility:
Decision variables can have fractional values.
(5) Deterministic (Certainty):
In the linear programming models, all the parameters are assumed to be known exactly.
(Source – Various books from the college library)
Copyrighted Material © 2019 - 2024 Prinsli.com - All rights reserved
All content on this website is copyrighted. It is prohibited to copy, publish or distribute the content and images of this website through any website, book, newspaper, software, videos, YouTube Channel or any other medium without written permission. You are not authorized to alter, obscure or remove any proprietary information, copyright or logo from this Website in any way. If any of these rules are violated, it will be strongly protested and legal action will be taken.



Be the first to comment