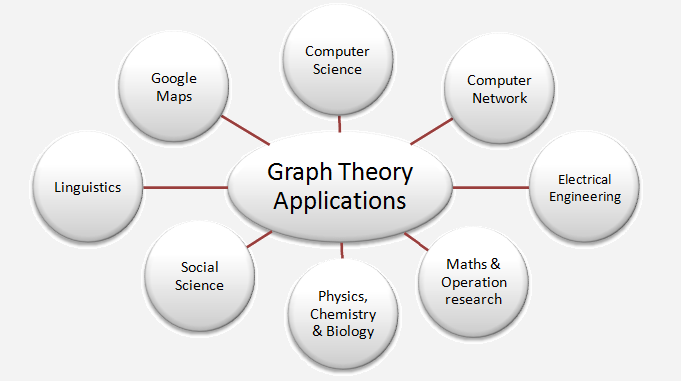
Graph Theory Applications in Hindi

Graph Theory Applications in Hindi (ग्राफ सिद्धांत के अनुप्रयोग):

ग्राफ सिद्धांत की आंतरिक सादगी के कारण, कंप्यूटर विज्ञान, कंप्यूटर नेटवर्क, इंजीनियरिंग विज्ञान, सामाजिक विज्ञान, गणित, भौतिकी, रसायन विज्ञान, जीव विज्ञान, आनुवंशिकी, अर्थशास्त्र, रसद, भाषा विज्ञान, समाजशास्त्रीय संरचना, डेटा संरचना, कृत्रिम खुफिया, पैटर्न पहचान, साइबरनेटिक्स, विश्वसनीयता सिद्धांत, कंप्यूटर दोष निदान सहित और कई अन्य क्षेत्रों में ग्राफ सिद्धांत के बहुत सारे अनुप्रयोग हैं। कंप्यूटर मेमोरी की संरचना का अध्ययन करने और मंगल ग्रह की नहरों के अध्ययन में भी ग्राफ सिद्धांत का उपयोग किया गया है। इस प्रकार, ग्राफ सिद्धांत अनुप्रयोगों की सूची बढ़ती जा रही है।

पहली बात जो ध्यान में रखनी चाहिए वह यह है कि ग्राफ एक गणितीय संरचना है जो रोजमर्रा की समस्याओं को ग्राफिकल तरीके से प्रस्तुत करने की अनुमति देता है। कंप्यूटर विज्ञान (एल्गोरिदम और संगणना), इलेक्ट्रिकल इंजीनियरिंग (संचार नेटवर्क और कोडिंग सिद्धांत), संचालन अनुसंधान (शेड्यूलिंग), और जैव रसायन (जीनोमिक्स) सहित विभिन्न क्षेत्रों में इसके अनुप्रयोगों के कारण, ग्राफ सिद्धांत तेजी से गणित की मुख्यधारा का हिस्सा बन रहा है।

ग्राफ सिद्धांत गणित की एक शाखा है जिसे कंप्यूटर विज्ञान में भी लागू किया जाता है। यह असतत गणित (discrete mathematics) और अनुप्रयुक्त गणित (applied mathematics) दोनों पर आधारित है। इस तरह, यह विभिन्न अवधारणाओं को शामिल करने में सक्षम है।

ग्राफ सिद्धांत अनुप्रयोगों के कुछ उदाहरण निम्नलिखित हैं:

1. कंप्यूटर विज्ञान (Computer Science) में ग्राफ सिद्धांत के अनुप्रयोग:

कंप्यूटर विज्ञान में, एक ग्राफ का उपयोग संचार के नेटवर्क, डेटा संगठन, कम्प्यूटेशनल उपकरणों आदि का प्रतिनिधित्व करने के लिए, और computation flow का वर्णन करने के लिए करने के लिए किया जाता है। ग्राफ ट्रांसफॉर्मेशन सिस्टम, ग्राफ के नियमों पर आधारित इन-मेमोरी ग्राफ मैनिपुलेशन पर काम करते हैं। ग्राफ डेटाबेस, ग्राफ संरचित डेटा के सुरक्षित लेन-देन, निरंतर भंडारण और क्वेरी के लिए अनुमति देते हैं।

♦ ग्राफ सिद्धांत का उपयोग एल्गोरिदम के अध्ययन के लिए भी किया जाता है। उदाहरण के लिए,

• Dijkstra’s Algorithm (दिज्क्स्ट्रा का एल्गोरिथम) – दिज्क्स्ट्रा का एल्गोरिथ्म कुशलतापूर्वक दो शीर्षों के बीच सबसे छोटा रास्ता खोजता है। यह वास्तविक दुनिया के बहुत सारे अनुप्रयोगों का आधार है।

लेकिन रूटिंग समस्याओं के कई और अनुप्रयोग भी हैं। उदाहरण के लिए, न्यूनतम फैले हुए पेड़ (minimum spanning tree) की समस्या। उद्देश्य – शीर्षों के बीच कनेक्शनों का एक न्यूनतम कुल भार (सबसे कम कुल भार) सेट खोजना है, ताकि ग्राफ़ के प्रत्येक शीर्ष से हर दूसरे शीर्ष तक एक पथ हो। इसे कुशलतापूर्वक पूरा करने के लिए क्रुस्कल या प्राइम के एल्गोरिदम का उपयोग किया जा सकता है। इसका एक वास्तविक उदाहरण, हब के बीच बिजली का जाल (Electricity network) है। बहुत सारे संभावित कनेक्शन हैं, लेकिन उनमें से सभी की आवश्यकता नहीं होती है। कम से कम (न्यूनतम) फैले पेड़ के कनेक्शन चुनने से लागत कम हो जाएगी।

• Kruskal’s Algorithm (क्रुस्कल का एल्गोरिथम) – क्रुस्कल एल्गोरिथम किसी दिए गए ग्राफ में हाथ और कंप्यूटर दोनों के द्वारा सबसे छोटे फैले हुए पेड़ को खोजने की एक विधि है।

• Prim’s Algorithm (प्राइम का एल्गोरिथम) – प्राइम एक और एल्गोरिदम है, जिसमें वजन घटाने के क्रम में सभी किनारों को सूचीबद्ध करने की या प्रत्येक चरण पर जांच करने की आवश्यकता नहीं है, यदि कोई नया चयनित किनारा सर्किट बनाता है।

♦ कंप्यूटर प्रोग्रामिंग में भी ग्राफ थ्योरी का प्रयोग किया जाता है।

कंप्यूटर प्रोग्रामिंग के शुरुआती दिनों से ही, किसी दिए गए कंप्यूटर प्रोग्राम का विश्लेषण एक महत्वपूर्ण समस्या रही है। किसी प्रोग्राम को digraph के रूप में प्रस्तुत करना बहुत सुविधाजनक है। प्रत्येक vertex एक प्रोग्राम ब्लॉक को दर्शाता है, और प्रत्येक edge (ν_i, ν_j) प्रोग्राम ब्लॉक ν_i में अंतिम निर्देश से प्रोग्राम ब्लॉक ν_j में पहले निर्देश पर नियंत्रण के संभावित हस्तांतरण को दर्शाता है। इस तरह के digraph को programme digraph कहा जाता है। एक programme digraph एक फ्लो चार्ट का एक सरलीकृत संस्करण है जिसमें boxes को vertices में सिकोड़ दिया जाता है और arrows को edges में बदल दिया जाता है।

2. कंप्यूटर नेटवर्क (Computer Network) में ग्राफ सिद्धांत के अनुप्रयोग:

• नेटवर्क में परस्पर जुड़े कंप्यूटरों के बीच संबंध ग्राफ थ्योरी के सिद्धांतों का पालन करते हैं।

कंप्यूटर नेटवर्क में, एक टोपोलॉजी का उपयोग यह समझाने के लिए किया जाता है कि नेटवर्क भौतिक रूप से कैसे जुड़ा है और साथ ही नेटवर्क में सूचना का तार्किक प्रवाह कैसे होता है। दूसरे शब्दों में, एक टोपोलॉजी मुख्य रूप से वर्णन करती है कि संचार लिंक का उपयोग करके डिवाइस कैसे जुड़े होते हैं,  एक दूसरे पर कैसे परस्पर प्रभाव डालते हैं और एक दूसरे के साथ बातचीत करते हैं।

• संचार के नेटवर्क का प्रतिनिधित्व करने के लिए ग्राफ सिद्धांत का उपयोग किया जाता है, साथ ही गणना प्रवाह (flow of computation) का वर्णन करने के लिए भी ग्राफ़ का उपयोग किया जाता है। नेटवर्क सुरक्षा भी ग्राफ सिद्धांत का उपयोग करती है।

• वर्टेक्स कलरिंग एल्गोरिथम (vertex colouring algorithm) का उपयोग, किसी भी जीएसएम (GSM – Grouped Special Mobile) मोबाइल फोन नेटवर्क के लिए अधिकतम चार अलग-अलग आवृत्तियों को असाइन करने के लिए किया जा सकता है। वर्टेक्स कलरिंग एल्गोरिथम का उपयोग चार रंगों के साथ मानचित्र के लिए उपयुक्त रंग खोजने के लिए किया जाता है।

3. इलेक्ट्रिकल इंजीनियरिंग (Electrical Engineering) में ग्राफ सिद्धांत के अनुप्रयोग:

इलेक्ट्रिकल इंजीनियरिंग में, सर्किट कनेक्शन को डिजाइन करने में ग्राफ सिद्धांत की अवधारणाओं का व्यापक रूप से उपयोग किया जाता है। इन सर्किट कनेक्शनों को टोपोलॉजी कहा जाता है।

[टोपोलॉजी (Topology) – दूसरे शब्दों में, टोपोलॉजी एक संचार नेटवर्क के तत्वों की व्यवस्था है। किसी नेटवर्क की टोपोलॉजी का उसके ग्राफ के माध्यम से अध्ययन किया जाता है। टोपोलॉजी के कुछ उदाहरण स्टार, ब्रिज, मेश, ट्री, रिंग, सर्कुलर, हाइब्रिड, सीरीज़ और समानांतर टोपोलॉजी हैं, जिनमें से प्रत्येक में नोड्स और लिंक के विभिन्न कॉन्फ़िगरेशन होते हैं। प्रत्येक व्यवसाय के लिए सर्वोत्तम नेटवर्क टोपोलॉजी उसके आकार, पैमाने, लक्ष्यों और बजट द्वारा निर्धारित की जाती है।]

चूंकि अलग प्रकार के विद्युत तत्व केवल कुछ ही हैं, नेटवर्क में भिन्नता मुख्य रूप से टोपोलॉजी में भिन्नता के कारण होती है। इस प्रकार, विद्युत नेटवर्क विश्लेषण और संश्लेषण मुख्य रूप से नेटवर्क टोपोलॉजी का अध्ययन है। विद्युत तत्वों की प्रकृति और आकार की परवाह किए बिना, विद्युत नेटवर्क का एक ग्राफ खींचने में, junctions को vertices से, और branches (जिसमें विद्युत तत्व होते हैं) को edges से दर्शाया जाता है।

4. गणित (Mathematics) में ग्राफ थ्योरी के अनुप्रयोग:

गणित में ग्राफ सिद्धांत, ज्यामिति और टोपोलॉजी के कुछ हिस्सों जैसे नॉट थ्योरी (knot theory), में उपयोगी होते हैं।

गणित में अध्ययन का एक महत्वपूर्ण क्षेत्र ऑपरेशन रिसर्च है। ऑपरेशन रिसर्च में उपयोगी अनुप्रयोगों के दो उदाहरण: minimum cost path (न्यूनतम लागत पथ या सबसे सस्ता मार्ग) और scheduling problem (शेड्यूलिंग समस्या) हैं, जिन्हें ग्राफ सिद्धांत द्वारा हल किया जाता है।

ऑपरेशन रिसर्च (Operation Research – OR) में ग्राफ थ्योरी के अनुप्रयोग:

ऑपरेशन रिसर्च, जैसे मॉडलिंग (modelling), परिवहन (transportation), नेटवर्क गतिविधि (network activity), गेम थ्योरी (game theory) आदि में, ग्राफ सिद्धांत की अवधारणाओं का व्यापक रूप से उपयोग किया जाता है।

• नेटवर्क गतिविधि का उपयोग करके, बड़ी संख्या में संयोजक समस्याओं (combinatorial problems) का समाधान किया जाता है।

• OR में नेटवर्क का सबसे लोकप्रिय और सफल अनुप्रयोगों में से एक ‘बड़ी जटिल परियोजनाओं की योजना और समय-निर्धारण’ है। PERT (Project Evaluation Review Technique – परियोजना मूल्यांकन समीक्षा तकनीक) और CPM (Critical Path Method – क्रिटिकल पाथ मेथड) दो सबसे प्रसिद्ध समस्याएं हैं।

• प्रतिस्पर्धी वातावरण में विशिष्ट कार्यों को करने का सबसे अच्छा तरीका (इष्टतम तरीका) खोजने के लिए, इंजीनियरिंग, अर्थशास्त्र, युद्ध विज्ञान आदि में समस्याओं के लिए गेम थ्योरी (game theory) लागू की जाती है। यहां, vertices स्थिति या जगह का प्रतिनिधित्व करते हैं और edges गतिविधियों का प्रतिनिधित्व करते हैं।

5. विज्ञान (Science) में ग्राफ सिद्धांत के अनुप्रयोग:

ग्राफ सिद्धांत भौतिकी, रसायन विज्ञान, जीव विज्ञान और संरक्षण के प्रयासों में भी उपयोगी है।

भौतिकी (Physics) और रसायन विज्ञान (Chemistry) में ग्राफ सिद्धांत के अनुप्रयोग:

• भौतिकी और रसायन विज्ञान में, अणुओं का अध्ययन करने के लिए ग्राफ सिद्धांत का उपयोग किया जाता है, क्योंकि ग्राफ किसी पदार्थ की आणविक और रासायनिक संरचनाओं आदि का प्रतिनिधित्व करते हैं।

• किसी भी अणु की आणविक संरचना और जाली (lattice) के निर्माण के लिए भी एक ग्राफ का उपयोग किया जा सकता है। यह परमाणुओं और अणुओं के बीच बंधन संबंध को दिखाने के साथ-साथ एक अणु की संरचना की दूसरे से तुलना करने में भी सहायता करता है।

• ग्राफ की सहायता से, परमाणुओं की टोपोलॉजी से संबंधित ग्राफ-सैद्धांतिक गुणों पर डेटा एकत्र करके जटिल सिम्युलेटेड (नकली) परमाणु संरचनाओं की 3डी संरचना का मात्रात्मक अध्ययन किया जा सकता है।

• सांख्यिकीय भौतिकी में, ग्राफ एक प्रणाली के परस्पर क्रिया करने वाले भागों के साथ-साथ ऐसी प्रणालियों पर एक भौतिक प्रक्रिया की गतिशीलता के बीच स्थानीय कनेक्शन का प्रतिनिधित्व कर सकते हैं।

जीव विज्ञान (Biology) में ग्राफ सिद्धांत के अनुप्रयोग:

• किसी जीव की डीएनए संरचना (DNA structure), जैविक नेटवर्क, तंत्रिका नेटवर्क आदि को दर्शाने के लिए, ग्राफ का उपयोग किया जाता है।

• जैविक नेटवर्क में नोड्स (vertices) जीन, प्रोटीन या मेटाबोलाइट्स जैसे द्वि-आणविक पदार्थों (bimolecular entities) का प्रतिनिधित्व करते हैं, और इन नोड्स को जोड़ने वाले edges, संबंधित द्वि-आणविक के बीच कार्यात्मक (functional), भौतिक या रासायनिक बातचीत (परस्पर प्रभाव) का प्रतिनिधित्व करते हैं।

• ग्राफ सिद्धांत का उपयोग मेटाबोलिक नेटवर्क (Metabolic networks) और ट्रांसक्रिप्शनल विनियमन नेटवर्क (transcriptional regulation networks) में भी किया जाता है।

• ग्राफ सिद्धांत PPI (प्रोटीन-प्रोटीन इंटरैक्शन) नेटवर्क और ड्रग-ड्रग लक्ष्य संबंधों (drug-drug target relationships) को चिह्नित करने में भी उपयोगी है।

6. सामाजिक विज्ञान (Social Science) में ग्राफ सिद्धांत के अनुप्रयोग:

समाजशास्त्र (Sociology) भी ग्राफ सिद्धांत का व्यापक उपयोग करता है। उदाहरण के लिए,

• लोग एक-दूसरे को जानते हैं या नहीं, yah janne के लिए, परिचितता और दोस्ती के ग्राफ़ (Acquaintanceship and friendship graphs) का उपयोग करना।

• अफवाह फैलाने का पता लगाने के लिए, या विशेष रूप से अभिनेताओं की प्रतिष्ठा को मापने के लिए, सामाजिक नेटवर्क विश्लेषण सॉफ्टवेयर (social network analysis software) का उपयोग करना।

• कुछ व्यक्तियों द्वारा दूसरों के व्यवहार को प्रभावित करने के लिए, प्रभाव ग्राफ मॉडल (influence graphs model) का उपयोग करना।

• यह जांचने के लिए कि क्या दो लोग एक विशेष तरीके से सहयोग करते हैं, जैसे कि एक टीम में एक साथ काम करना, सहयोग ग्राफ़ मॉडल (collaboration graphs model) का उपयोग करना।

• एक समाज या समूह में लोगों के बीच संबंधों का प्रतिनिधित्व करने के लिए sociogram का उपयोग करना, जहां sociogram एक digraph (निर्देशित ग्राफ) है जो किसी व्यक्ति के सामाजिक कनेक्शन का प्रतिनिधित्व करता है। एक sociogram में, vertices सदस्यों को दर्शाते हैं और directed edges संबंधों (प्रशंसा, जुड़ाव, प्रभाव, आदि) को दर्शाते हैं। मानवविज्ञानियों ने अनेक जनजातियों का अध्ययन किया है और उनकी रक्त-संबंध संरचनाओं (kinship structures) के आधार पर उनका वर्गीकरण किया है।

7. भाषाविज्ञान (Linguistics) में ग्राफ सिद्धांत के अनुप्रयोग:

भाषाविज्ञान भाषा का विज्ञान है, जिसमें शब्दार्थ, वाक्य-विन्यास, ध्वनि-विज्ञान, स्वर-विज्ञान, किसी भाषा की ध्‍वनि-प्रणाली, शब्द-साधन (शब्द के भागों का विज्ञान), व्यावहारिकता, ऐतिहासिक भाषाविज्ञान आदि शामिल हैं। भाषाविज्ञान में, ग्राफ का उपयोग diagrams का parsing वर्णन करने के लिए किया जाता है। Vertices, शब्दों और शब्द तार (वाक्य) को दर्शाते हैं, जबकि edges उनके बीच कुछ वाक्यात्मक संबंधों को दर्शाते हैं।

शब्दों का एक समूह (vocabulary) और नियमों का एक समूह (grammar), स्ट्रिंग्स (वाक्य – sentences) बनाने के लिए एक भाषा को परिभाषित करता है, अर्थात्, भाषा सभी कानूनी रूप से उत्पन्न स्ट्रिंग्स (वाक्यों) का एक संग्रह है। कम्प्यूटेशनल भाषाविज्ञान में, एक समस्या यह पहचानना है कि दी गई स्ट्रिंग (वाक्य) उस भाषा से संबंधित है या नहीं, जिसकी शब्दावली (vocabulary) और व्याकरण (grammar) दी गई है।

• भाषाविज्ञान में, ग्राफ का उपयोग ज्यादातर किसी भाषा के पार्सिंग ट्री और किसी भाषा के व्याकरण के लिए किया जाता है। (एक rooted, ordered tree जो एक स्ट्रिंग की वाक्य रचनात्मक संरचना का प्रतिनिधित्व करता है उसे एक पार्सिंग ट्री कहा जाता है)।

• शब्दार्थ नेटवर्क (Semantics networks) का उपयोग शाब्दिक शब्दार्थ (lexical semantics) के भीतर किया जाता है, विशेष रूप से जब कंप्यूटर पर लागू किया जाता है, क्योंकि मॉडलिंग शब्द का अर्थ तब आसान होता है जब किसी दिए गए शब्द को संबंधित शब्दों के संदर्भ में समझा जाता है।

• एक ग्राफ के रूप में भाषा के विश्लेषण में, अक्सर स्वर विज्ञान (ध्‍वनि-प्रक्रिया, या किसी भाषा की ध्‍वनि-प्रणाली, या phonology) और शब्द-साधन (शब्द के भागों का विज्ञान, या morphology) विधियों का उपयोग किया जाता है।

8. गूगल मैप्स (Google Maps) में ग्राफ सिद्धांत के अनुप्रयोग:

ग्राफ़ सिद्धांत का उपयोग किसी नेटवर्क या सड़क पर सबसे छोटा मार्ग खोजने के लिए किया जाता है। उदाहरण के लिए, जीपीएस द्वारा घर के लिए सबसे छोटा रास्ता खोजने के लिए ग्राफ सिद्धांत का उपयोग किया जाता है। Google मानचित्र में, विभिन्न स्थानों को कोनों, शीर्षों या नोड्स (vertices or nodes) के रूप में दर्शाया जाता है, और सड़कों को किनारों (edges) के रूप में दर्शाया जाता है, जिसमें दो vertices के बीच सबसे छोटा रास्ता खोजने के लिए ग्राफ़ सिद्धांत का उपयोग किया जाता है।

Read Also: Application of Graph Theory in Real Life in Hindi

(Source – Various books from the college library)

Read this article in ‘English’

ग्राफ सिद्धांत के कई अन्य अनुप्रयोग हो सकते हैं जिन्हें हो सकता है कि हम इस लेख में भूल गए हों, यदि आप हमें इस विषय के बारे में और बताना चाहते हैं, तो Please Comment.

Tags: graph theory and its applications, graph theory with applications to engineering and computer science, chemical applications of graph theory, application of graph theory in real life, real world applications of graph theory, application of graph theory in various fields, application of graph theory in social media, applications of graph theory to landscape genetics

Copyrighted Material © 2019 - 2024 Prinsli.com - All rights reserved

All content on this website is copyrighted. It is prohibited to copy, publish or distribute the content and images of this website through any website, book, newspaper, software, videos, YouTube Channel or any other medium without written permission. You are not authorized to alter, obscure or remove any proprietary information, copyright or logo from this Website in any way. If any of these rules are violated, it will be strongly protested and legal action will be taken.