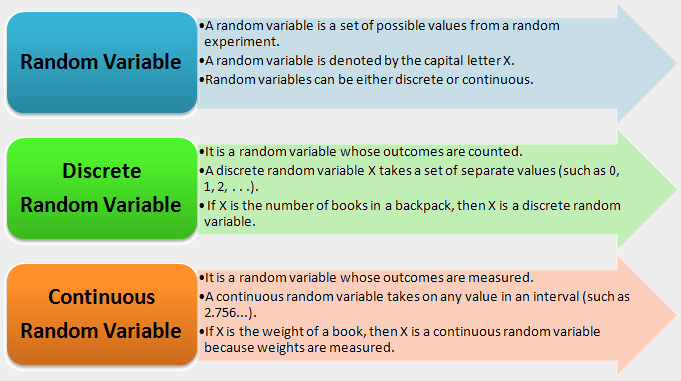
Random Variable Definition

Introduction of Random Variable:

In algebra, a variable is a number or quantity that are unknown. The type of variable you are using in algebra is a lowercase x or y. Here, variables like “x”, “y”, etc. signify an unknown quantity like y= 2x-1, because you solve y= 2x-1 for the value of x, where x represents a special number or set of numbers.

Then there’s statistics, where various types of variables, including random variables, are used. If an uppercase X or Y is shown, it is a random variable that usually refers to the probability of achieving a particular result. Although random variables are still quantities, they differ from “x” and “y” (which are merely numbers), because random variables have distinct characteristics and behaviours.

Definition of Random Variable:

The meaning of “Random” is “Unpredictable”. As a result, a random variable is one whose value in future is not foreseen or predictable even when its past performance is known.

We know that the numerical values that a variable takes are the outcome of some random event with suitable methods of data collection. In short, a random variable is a numerical value of the result of a random event. For example, the randomness may come from choosing a random sample from a population or doing a truly random experiment. In such conditions, the variable is known as a random variable. 

In other words, if a variable takes different values depending on the outcomes of a random experiment, it is said to be a random variable. A random variable is so named as random because we have no idea ahead of time exactly what value it will have after the experiment. For example, when we flip a coin, we have no way of knowing for sure whether it will fall heads or tails.

In other words, a random variable describes the results of a statistical experiment. The values of a random variable can change with each trial or repetition of an experiment.

Random Variable Notation:

To denote variables, letters near the end of the alphabet, such as x, can be used. For the possible value of a random variable also, we will use lowercase letters like x. But to denote the random variable itself rather than a special value, we will use an uppercase letter, such as X.

In other words, a random variable is denoted by the capital letter X, and the value of a random variable is denoted by lower case letters such as x or y.

Hence, if X is a random variable, then we write X in words and express the value of x as a number.

Example:

Let us toss three coins and count the number of heads. In this case, the sample space for tossing three coins is,

{TTT, THH, HTH, HHT, HTT, THT, TTH, HHH}.

Here, the number of heads can be 0, 1, 2 or 3. Then x = 0, 1, 2, 3 is the result.

Hence, the random variable is denoted by the uppercase letter X, where X = number of heads in three coin tosses, whereas x = 1 is one of its possible values as are x = 3, x= 2 and x = 0. Here, x is a number and X is in word.

It’s worth noting that the x values in this case are countable outcomes. X is a discrete random variable since the possible values for X may be counted as whole numbers and the outcomes are random (the x values 0, 1, 2, 3).

Types of Random Variable:

Random variables are classified according to their probability distribution. A random variable is related to either a probability distribution (Discrete Random Variable) or a probability density function (Continuous Random Variable). As a result, there are two types of random variables:

1. Discrete Random Variables, and
2. Continuous Random Variables.

(1) Discrete Random Variables:

A discrete random variable is a random variable whose outcomes are counted.

A discrete random variable X can take only a set of separate numbers (such as 0, 1, 2, . . .), or in other words, it can only take a finite number of different values.

For example, in a group of 4 people, the number of people who received at least one gift would be 0, 1, 2, 3, or 4. It cannot be a number between any of these values, like 3.665. Hence, discrete random variables can take on only a countable number of separate values.

Discrete random variables are involved in the Binomial and Poisson distributions.

♦ Examples of discrete random variables:

The number of heads when throwing three coins, the number of marbles in a jar, the number of broken bulbs in a box, the number of students in a class, the number of family members, etc. are all examples of discrete random variables because the outcomes in each case are counted only, not measured, that is, the outcomes can only occur a certain number of times.

(2) Continuous Random Variables:

A continuous random variable is a random variable whose outcomes are measured.

A continuous random variable takes on any value in an interval (such as 2.756…), or in other words, when the possible values of a random variable form an interval, it is called a continuous random variable. Hence, a random variable X is called a continuous random variable in a given interval (a, b) if it can take any value in that interval. Generally, these are measurements like height, weight, temperature, and the amount of time it takes to complete a task.

For example, it is analyzed in recent research how long people spend commuting to work, and this commuting time can be measured as a set of real numbers, such as between 0 to 90 minutes. The exact time may be 13.568, 78.352, or 83.815 minutes, or any of an infinite number of other values within this time range.

Continuous random variables are involved in the Normal distributions.

♦ Examples of continuous random variables:

The height of trees in the forest, IQ scores, cricket batting averages, the duration of a long-distance phone conversation, the amount of money a person carries, the lifespan of a computer chip, SAT results, etc. are all examples of continuous random variables because the outcomes in each case are measured, that is, the outcomes form an interval it can take any value in that interval.

◊ Important Remark for Discrete & Continuous random variables:

It is possible for the values of discrete and continuous random variables to be unclear or ambiguous.

• For example, X is a discrete random variable if X equals the number of miles (to the nearest mile) you travel to work because in this case, you count the miles. But X is a continuous random variable if X is the distance you drive to work because in this case, you measure values of X.

• Also, for example, X is a discrete random variable if X is the number of books in a bag. But X is a continuous random variable if X is the weight of a book.

(Source – Various books from the college library)

Copyrighted Material © 2019 - 2024 Prinsli.com - All rights reserved

All content on this website is copyrighted. It is prohibited to copy, publish or distribute the content and images of this website through any website, book, newspaper, software, videos, YouTube Channel or any other medium without written permission. You are not authorized to alter, obscure or remove any proprietary information, copyright or logo from this Website in any way. If any of these rules are violated, it will be strongly protested and legal action will be taken.