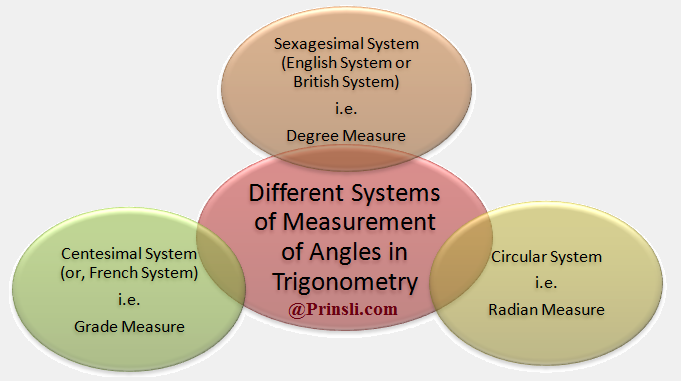
Different Systems of Measurement of Angles in Trigonometry:
Sexagesimal System, Centesimal System and Circular System are 3 different systems of Measuring Angle in Trigonometry: Angles in geometry are measured in terms of a right angle. The Right Angle serves as the foundation for defining the various systems for measuring angles. However, due to its size, this is an inconvenient unit of measurement. Generally, 3 different systems are used to measure angles. Following are the 3 different systems of measuring angle:
(1) Sexagesimal System ( or English System or British System)
(2) Centesimal System ( or French System)
(3) Circular System (Radian Measure)
Read Also: Measurement of Angles (All Basic Knowledge)
(1) Sexagesimal System (Degree Measure):
An angle is measured in Degrees, Minutes and Seconds in the Sexagesimal system.
The Sexagesimal system is the most popular and widely used measurement system to measure angles. In this system, a Right Angle is divided into 90 equal parts known as Degrees. Also in this system, each degree is subdivided into 60 equal parts called Minutes, and each minute is subdivided into 60 equal parts known as Seconds.
A degree is denoted by the symbol 1°, a minute is denoted by the symbol 1′, and a second is denoted by the symbol 1″. As a result, we get
1 Right Angle = 90 Degrees (90°)
1 Degree (1°) = 60 Minutes (60′)
1 Minute (1′) = 60 Seconds (60″)
Sexagesimal System is a well-established system that is always used in practical trigonometry applications. It is, however, not very convenient due to the multipliers 60 and 90.
(2) Centesimal System (Grade Measure):
An angle is measured in Grades, Minutes and Seconds in the Centesimal system.
The Centesimal System is another measurement system to measure angles in trigonometry. In this system, a Right Angle is divided into 100 equal parts known as Grades. Also in this system, each grade is subdivided into 100 equal parts called Minutes, and each minute is subdivided into 100 equal parts known as Seconds.
A grade is denoted by the symbol 1g, a minute is denoted by the symbol 1′, and a second is denoted by the symbol 1″. As a result, we get
1 Right Angle = 100 Grades (100g)
1 Grade (1g) = 100 Minutes (100′)
1 Minute (1′) = 100 Seconds (100″)
Centesimal System would be far more user-friendly and convenient than the standard Sexagesimal System. However, before it could be implemented, a large number of tables would have to be recalculated. For this reason, the system has never been used in practice.
Important Remark:
1. It is obvious that minutes and seconds differ in sexagesimal and centesimal systems.
2. To convert Sexagesimal into Centesimal Measure: If the angle does not have an integral number of degrees, it can be reduced to a fraction of a degree before being converted to grades.
(3) Circular System (Radian Measure):
An angle is measured in Radian in the Circular system.
Circular System is the third measurement system of measuring angles that have been devised, and it is used in all higher branches of mathematics and in other applications of Science. The unit used in the Circular System is obtained as follows:
- First, we draw any circle whose centre is O, as shown below figure.
- Then from any point ‘A’ on the circle, we measure off an arc AP whose length equals the radius of the circle.
- Then join the OA and OP.
- Then we obtain an angle AOP.

- The angle AOP is the angle that is used as the unit of circular measurement, that is, it is the angle in terms of which in this system all others are measured.
- This angle is known as A Radian or 1 Radian and is commonly denoted by 1c.
The symbol ‘c’ is usually omitted in practice, and an angle “π” is written instead of an angle “πc.”
Hence, A radian (rad) is the measure of the central angle subtended by an arc of a circle equal to the circle’s radius. The radian is a constant angle.
Why Radian is a constant angle: It is obviously necessary for the proper selection of a unit that it is a constant quantity; so we must demonstrate that the Radian is a constant angle.
Obviously, it is no matter how big or small the circles are, the quantity ‘Circumference/Diameter’ is always the same for all circles. In other words, the ratio ‘Circumference/Diameter’ is always equal for all circles, regardless of their sizes. Hence, the ratio of the circumference of a circle to its radius, and therefore also to its diameter, is a constant quantity.
The value of this constant quantity or ratio ‘Circumference/Diameter’ is always denoted by the Greek letter π [pronounced “Pi”], so π is a number. That is,
Circumference/Diameter = π (a constant number)
As a result, we obtain the following theorem:
The circumference of a circle is always equal to π times its diameter or 2π times its radius.
Approximate value of Pi (π): Unluckily, the value of π is not a whole number. It also cannot be expressed as a vulgar fraction, and thus cannot be expressed as a terminating or recurring decimal number. The constant number π is an incommensurable magnitude, which means that its value cannot be exactly expressed as the ratio of two whole numbers.
- An approximate value of π, correct to 2 places of decimals is the fraction 22/7= 3.14…
- An approximate value of π correct to 6 places of decimals is the fraction 355/113= 3.141592…
- A more accurate value of π correct to 8 decimal places is 3.14159265…
By division, we obtain 1/π= 0.3183098862 …
Read Also: The great Indian mathematicians Aryabhatta, & what is π, value and calculation of Pi (π)
The magnitude of a Radian: Let the arc be a semi-circle i.e. half of the circumference, as shown in the below figure. Hence, the length of the arc
will be
, where
is the radius of the circle.
We know that angles at the centre of any circle are to one another as the arcs on which they stand. Hence,
But we defined the to be a 1 Radian, Hence,
Also, we can say that if
Then,
So, we get,
And,
Hence, a full rotation in a circle equals 360° or 2π radians or 400 grades.
Radian measure is more suitable for conversion, analysis and calculations compare to Degree measure.
In other words, we can say that the Radian measurement of an angle is more convenient for analysis, whereas the Degree measurement of an angle is better for communicating the concept between people.
Since the number π arose from the circumference of a circle and so π plays an important role in radian measurement.
Hence, a relationship between Degree, Radian and Grade are defined as follows:
- 1 degree = π/180 radians = 10/9 grades,
- 1 radian = 180/π degrees = 200/π grades,
- 1 grade = 0.9 degrees = π/200 radians.
And, also,
A Right Angle = 90° = π/2 rad = 100 grad,
A Straight Angle = 180° = π rad = 200 grad,
A Full Rotation = 360° = 2π rad = 400 grad.
Tags: relation between sexagesimal system centesimal and circular systems to measure angle, define sexagesimal system centesimal and circular systems measuring angle, sexagesimal measure of angle in trigonometry, sexagesimal system in trigonometry, centesimal measure of angle in trigonometry, centesimal system in trigonometry, circular measure of angle in trigonometry, circular system in trigonometry, sexagesimal system centesimal circular systems angle
Copyrighted Material © 2019 - 2024 Prinsli.com - All rights reserved
All content on this website is copyrighted. It is prohibited to copy, publish or distribute the content and images of this website through any website, book, newspaper, software, videos, YouTube Channel or any other medium without written permission. You are not authorized to alter, obscure or remove any proprietary information, copyright or logo from this Website in any way. If any of these rules are violated, it will be strongly protested and legal action will be taken.










Be the first to comment