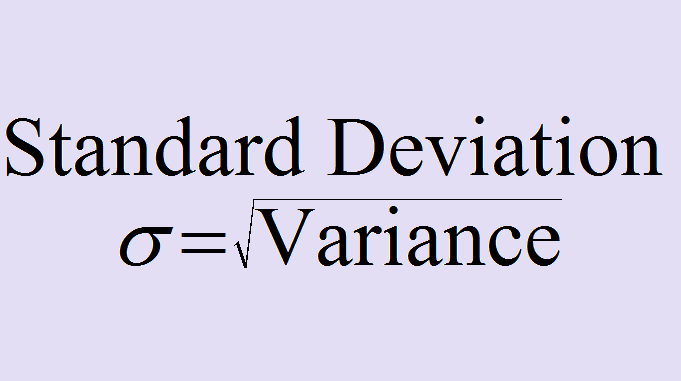
Standard Deviation (S.D.) in Hindi: Definition and Formula

Lata Agarwal Business Statistics & Statistics
standard deviation formula hindi

Standard Deviation in Hindi

मानक विचलन या प्रमाप विचलन (Standard Deviation in Hindi):

प्रसरण (variance) का धनात्मक वर्गमूल मानक विचलन है। इसलिये,

मानक विचलन σ = √ (प्रसरण)

मानक विचलन, जिसे ग्रीक अक्षर σ (सिग्मा के रूप में पढ़ा जाता है) द्वारा निरूपित किया जाता है, माध्य के प्रतिनिधित्व और उसके मूल्यांकन को समझने में अत्यधिक सहायक और उपयोगी होता है। प्रसरण प्रसार का एक अस्पष्ट विचार देता है, जबकि मानक विचलन अधिक स्पष्ट विचार देता है, जो माध्य से सटीक दूरी बताता है। मानक विचलन फैलाव का एक विशेष रूप से महत्वपूर्ण उपाय है क्योंकि यह कुछ प्रकार के वितरणों के लिए माध्य के दोनों ओर निश्चित दूरी के भीतर डेटा मानों के अनुपात को निर्धारित करने का आधार है।

Read this article in English

कार्ल पियर्सन ने मानक विचलन के नियम को प्रस्तुत किया। मानक विचलन के इस सिद्धांत का व्यावहारिक महत्व है क्योंकि यह परिसर (range), चतुर्थक विचलन (quartile deviation) और माध्य विचलन (average deviation) में पायी जाने वाली सभी त्रुटियों और दोषों से मुक्त है।

मानक विचलन की गणना करने के लिए, वास्तविक माध्य से लिए गए वर्ग विचलन के औसत का वर्गमूल उपयोग किया जाता है। इसे “मूल माध्य वर्ग विचलन” भी कहते हैं। सांख्यिकी में, प्रसरण को मानक विचलन के वर्ग के रूप में या σ2 के रूप में परिभाषित किया गया है।

कच्चे (अपरिष्कृत) डेटा के संदर्भ में, मानक विचलन की गणना:

अपरिष्कृत डेटा (raw data) के लिए, मानक विचलन की गणना के चार तरीके हैं:

(i) जब वास्तविक मान लिए जाते हैं;

(ii) जब विचलन वास्तविक माध्य से लिया जाता है;

(iii) जब विचलन कल्पित माध्य से लिया जाता है; तथा

(iv) जब कल्पित माध्य से ‘step deviation’ लिया जाता है।

मानक विचलन σ की गणना के लिए स्टेप्स :

(i) सबसे पहले दिए गए मानों या डेटा के सरल माध्य की गणना करें।

(ii) फिर दिए गए मानों का वर्ग करें और उन्हें जोड़ें।

(iii) अंत में, मानक विचलन σ का मान ज्ञात करने के लिए सूत्र (formula) का उपयोग करें।

मानक विचलन की गणना के लिए सूत्र (Standard Deviation Formulas in Hindi):

  • अवर्गीकृत डेटा के लिए मानक विचलन:

(i) जब विचलन वास्तविक माध्य से लिया जाय:

\sigma = \sqrt {\frac{{\sum {{\left( {X - \overline X } \right)}^2}}}{N}} = \sqrt {\frac{{\sum {X^2}}}{N} - {{\left( {\frac{{\sum X}}{N}} \right)}^2}} = \sqrt {\frac{{\sum {X^2}}}{N} - {{\left( {\overline X } \right)}^2}},

जहाँ N = प्रेक्षणों की संख्या,

X= श्रेणी में दिये गए प्रेक्षण, और

\overline X = प्रेक्षणों का माध्य. 

(ii) जब विचलन कल्पित माध्य से लिया जाय:

\sigma = \sqrt {\frac{{\sum {d^2}}}{N} - {{\left( {\frac{{\sum d}}{N}} \right)}^2}},

जहाँ d = X - A, और A कल्पित माध्य है।

  • वर्गीकृत डेटा के लिए मानक विचलन:

(i) जब विचलन वास्तविक माध्य से लिया जाय:

\sigma = \sqrt {\frac{{\sum f{{\left( {X - \overline X } \right)}^2}}}{N}} = \sqrt {\frac{{\sum f{X^2}}}{N} - {{\left( {\frac{{\sum fX}}{N}} \right)}^2}} = \sqrt {\frac{{\sum f{X^2}}}{N} - {{\left( {\overline X } \right)}^2}}

(ii) जब विचलन कल्पित माध्य से लिया जाय:

\sigma = \sqrt {\frac{{\sum f{d^2}}}{N} - {{\left( {\frac{{\sum fd}}{N}} \right)}^2}} \times i,

जहाँ, d = X - A

  • प्रथम n प्राकृत संख्याओं के लिए मानक विचलन:

\sigma = \sqrt {\frac{1}{{12}}\left( {{N^2} - 1} \right)}

  • मानक विचलन का गुणांक

= \frac{\sigma }{{\overline X }}

  • विचरण का गुणांक:

C.V. = \frac{\sigma }{{\overline X }} \times 100

  • विचलनों की माप के बीच संबंध:

Q.D. = \frac{2}{3}\sigma, and

A.D. = \frac{4}{5}\sigma.

मानक विचलन के लिए अतिरिक्त महत्वपूर्ण नोट:

  • डेटा सेट 12, 12, 12, 12, 12 का मानक विचलन शून्य है (क्योंकि इस डेटा सेट में सभी मान समान हैं, यानी संख्याएं एकसमान हैं)।
  • मानक विचलन शून्य नहीं हो सकता जब तक कि डेटा सेट के सभी मानों का मान समान न हो (उदाहरण के लिए, 12, 12, 12, 12, 12, 12)।
  • मानक विचलन अपरिवर्तित रहता है यदि सभी मानों में समान संख्या को जोड़ा या घटाया जाए। उदाहरण के लिए, डेटा “34, 65, 45” का मानक विचलन डेटा “134, 165, 145” के समान होगा, क्योंकि मानक विचलन प्रेक्षणों और माध्य के बीच के अंतर पर निर्भर करता है, और प्रत्येक डेटा मान में 100 जोड़ने से माध्य भी 100 बढ़ जाता है।

Copyrighted Material © 2019 - 2024 Prinsli.com - All rights reserved

All content on this website is copyrighted. It is prohibited to copy, publish or distribute the content and images of this website through any website, book, newspaper, software, videos, YouTube Channel or any other medium without written permission. You are not authorized to alter, obscure or remove any proprietary information, copyright or logo from this Website in any way. If any of these rules are violated, it will be strongly protested and legal action will be taken.

About Lata Agarwal 270 Articles
M.Phil in Mathematics, skilled in MS Office, MathType, Ti-83, Internet, etc., and Teaching with strong education professional. Passionate teacher and loves math. Worked as a Assistant Professor for BBA, BCA, BSC(CS & IT), BE, etc. Also, experienced SME (Mathematics) with a demonstrated history of working in the internet industry. Provide the well explained detailed solutions in step-by-step format for different branches of US mathematics textbooks.
Website Facebook LinkedIn

Related Articles

objective of statistics, definition of statistics
Business Statistics & Statistics

Requisites of a Good Average in Hindi

Lata Agarwal Business Statistics & Statistics

Requisites of a Good Average in Hindi – अच्छे माध्य के आवश्यक तत्व – माध्य को स्पष्ट रूप से परिभाषित होना चाहिए, जिससे कि उसका एक ही अर्थ […]

Application of Statistics in Business and Management
Business Statistics & Statistics

Importance and Application of Statistics in Business and Management in Hindi

Lata Agarwal Business Statistics & Statistics

Importance and Application of Statistics in Business and Management in Hindi: व्यावसायिक समस्याओं को हल करने के लिए सांख्यिकीय विधियों का … […]

What are Vital statistics in hindi, Meaning and definition of Vital statistics in Hindi, Difference between Population Census and Vital Statistics
Business Statistics & Statistics

जीवन समंक क्या है? जीवन समंकों का अर्थ और परिभाषा

Lata Agarwal Business Statistics & Statistics

जीवन समंक क्या है? जीवन समंकों का अर्थ और परिभाषा (What are Vital statistics? Meaning and definition of Vital statistics in Hindi) …. […]

Be the first to comment

Leave a Reply

Your email address will not be published.


*