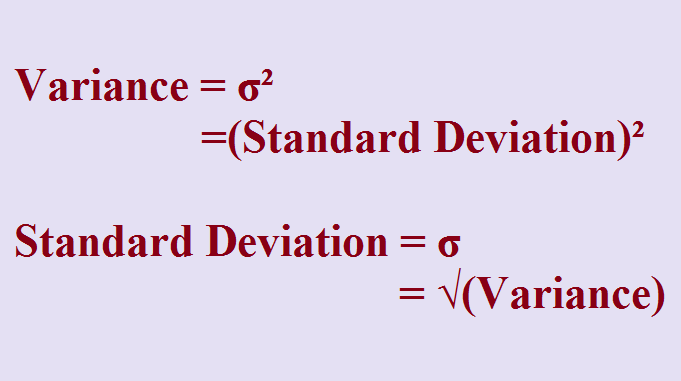
Definition of Variance in Statistics and Variance Formula

Lata Agarwal Business Statistics & Statistics
variance in statistics, variance formula

Definition of Variance in Statistics and Variance formula

Definition of Variance:

The square of standard deviation i.e. σ² is called ‘variance’ in statistics. Hence, 

Variance = σ², or σ = √(Variance)

The variance (Var.), a common measure of dispersion, includes all data values and is calculated by a mathematical formula. Variance measures how far a data set is spread out.

The technical definition of variance: “The variance is the average of the squared differences between the N data values and the mean,” but all it really does is give you a very general idea of the spread of your data.

A variance of zero means that there is no variability; all the numbers in the data set are the same.

Examples:

  • The data set 12, 12, 12, 12, 12 has a variance of zero, because all numbers are identical.
  • The data set 12, 12, 12, 12, 13 has a variance of 0.167; a small change in the numbers equals a very small variance.
  • The data set 12, 12, 12, 12, 13013 has a variance of 28171000; a large change in the numbers equals a very large number.

Steps for calculating Variance σ² :

(i) First calculate the simple mean of the given values or data.

(ii) Then, square the given values ​​and add them.

(iii) Finally, use the formula to get the variance σ².

Some formulas for Variance are as follows:

♦ Variance for Ungrouped Data:

(i) Deviations taken from Actual Mean:

{\sigma ^2} = \frac{{\sum {{{\left( {X - \overline X } \right)}^2}} }}{N} = \frac{{\sum {{X^2}} }}{N} - {\left( {\frac{{\sum X }}{N}} \right)^2} = \frac{{\sum {{X^2}} }}{N} - {\left( {\overline X } \right)^2}, 

where N= Number of the items,

X= The value given in the series, and

\overline X = Mean of the values. 

(ii) Deviations taken from Assumed Mean:

{\sigma ^2} = \frac{{\sum {{d^2}} }}{N} - {\left( {\frac{{\sum d }}{N}} \right)^2},

where d = X - A, and A is assumed mean.

♦ Variance for Grouped Data:

(i) Deviations taken from Actual Mean:

{\sigma ^2} = \frac{{\sum {f{{\left( {X - \overline X } \right)}^2}} }}{N} = \frac{{\sum {f{X^2}} }}{N} - {\left( {\frac{{\sum {fX} }}{N}} \right)^2} = \frac{{\sum {f{X^2}} }}{N} - {\left( {\overline X } \right)^2}

(ii) Deviations taken from Assumed Mean:

{\sigma ^2} = \frac{{\sum {f{d^2}} }}{N} - {\left( {\frac{{\sum {fd} }}{N}} \right)^2} \times i,

where, d = X - A

♦ Variance for first n natural numbers:

{\sigma ^2} = \frac{1}{{12}}\left( {{N^2} - 1} \right)

Additional Important Notes for Variance:

1. The variance of the data set 12, 12, 12, 12, 12 is zero (because all values in this data set are the same, that is, the numbers are identical).

2. The variance cannot be zero unless all values in a data set have the same value (e.g., 12, 12, 12, 12, 12, 12).

3. The variance remains unchanged if the same number is added to or subtracted from all of the values.
For example, the data “34, 65, 45” will have the same variance as data “134, 165, 145”. Because variance depends on the differences between the observations and the mean, and adding 100 to each data value increases the mean also by 100.

(Source – Various books from the college library)

Tags: what is the definition of variance in statistics and write the variance formula

Copyrighted Material © 2019 - 2024 Prinsli.com - All rights reserved

All content on this website is copyrighted. It is prohibited to copy, publish or distribute the content and images of this website through any website, book, newspaper, software, videos, YouTube Channel or any other medium without written permission. You are not authorized to alter, obscure or remove any proprietary information, copyright or logo from this Website in any way. If any of these rules are violated, it will be strongly protested and legal action will be taken.

About Lata Agarwal 270 Articles
M.Phil in Mathematics, skilled in MS Office, MathType, Ti-83, Internet, etc., and Teaching with strong education professional. Passionate teacher and loves math. Worked as a Assistant Professor for BBA, BCA, BSC(CS & IT), BE, etc. Also, experienced SME (Mathematics) with a demonstrated history of working in the internet industry. Provide the well explained detailed solutions in step-by-step format for different branches of US mathematics textbooks.
Website Facebook LinkedIn

Related Articles

principles of data classification in statistics
Business Statistics & Statistics

Principles of Data Classification

Lata Agarwal Business Statistics & Statistics

The classes can be more than 15 depending upon the total number of observations in the data and the details required, but they should not be less than 5 because, in this case, the classification may not reveal the essential characteristics. […]

Utility of Correlation and Significance of the study of Correlation
Business Statistics & Statistics

Correlation in Hindi – सहसंबंध, सहसंबंध गुणांक, सहसंबंध विश्लेषण

Lata Agarwal Business Statistics & Statistics

Correlation in Hindi – दो सांख्यिकीय चरों के बीच सम्बन्ध का माप सहसम्बन्ध (Correlation) कहलाता है। इससे पता चलता है कि दो चर आपस में … […]

difference between correlation and causation
Business Statistics & Statistics

Difference between Correlation and Causation in Statistics

Lata Agarwal Business Statistics & Statistics

The term “correlation” should not be confused with “causation.” If two variables have a correlation, it cannot be assumed that a change… […]

Be the first to comment

Leave a Reply

Your email address will not be published.


*