What is factorial n and how is it denoted? What is factorial of 100?

What is factorial n and how is it denoted?

In mathematics, the factorial is the product of all natural numbers less than or equal to a given positive integer, and it is denoted by that integer and an exclamation mark. Thus, factorial n is written as n!, meaning,

n! = 1 × 2 × 3 × … × (n−2) × (n−1) × n.

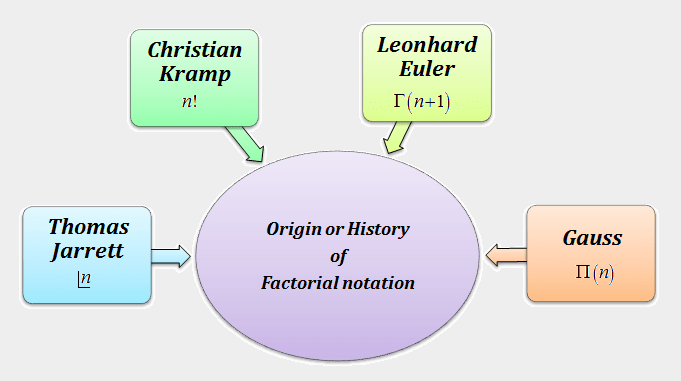
Notation of Factorial:

Factorial n is represented by several symbols.

• Generally, factorial n is denoted by the integer n and an exclamation point, that is, by the symbol,

n!

• Factorial n can also be denoted by the symbol, 

It is read as factorial n, or n factorial.

• In Many books, it is sometimes denoted by the symbol Γ(n+1), where

Γ(n+1) = n!

It is read as gamma n+1.

• In some books, especially in Germany, factorial n is denoted by the symbol ∏n (here, ∏ is a greek letter and may be thought of as standing for the product).

Hence, finally we get the following formula for factorial n:

∏n = Γ(n+1) = n! = |_n = n×(n−1)×(n−2)× . . . ×3×2×1.

Definition of factorial:

Simply, a product of the first n natural numbers (that is, the product of n consecutive integers beginning with 1 and ending with n) is called factorial n and denoted by n!. In other words, the factorial of non-negative integer n is the product of all positive integers less than or equal to n. It is denoted by n!.

That is, in mathematical words, factorial n, or, n factorial for all natural numbers n is defined as follows:

“n! = n×(n−1)×(n−2)× … ×3×2×1,

or,

n! = n · (n−1) · (n−2) · … · 3 · 2 · 1

And,

0! = 1.”

For example,

5! = 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 120.

Factorial formula:

If n is a natural number greater than or equal to 1, then,

n! = n×(n−1)×(n−2)× … ×3×2×1.

If n = 0, then n! = 0! = 1, by convention.

Examples of factorial n:

The factorials of first 11 natural numbers are as follows:

• Value of factorial 0, or 0 factorial, or 0! is,

0! = 1

• Value of factorial 1, or 1 factorial, or 1! is,

1! = 1

• Value of factorial 2, or 2 factorial, or 2! is,

2! = 2 ⋅ 1 = 2

• Value of factorial 3, or 3 factorial, or 3! is,

3! = 3 ⋅ 2 ⋅ 1 = 6

• Value of factorial 4, or 4 factorial, or 4! is,

4! = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24

• Value of factorial 5, or 5 factorial, or 5! is,

5! = 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 120

• Value of factorial 6, or 6 factorial, or 6! is,

6! = 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 720

• Value of factorial 7, or 7 factorial, or 7! is,

7! = 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 5,040

• Value of factorial 8, or 8 factorial, or 8! is,

8! = 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 40,320

• Value of factorial 9, or 9 factorial, or 9! is,

9! = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 3,62,880

• Value of factorial 10, or 10 factorial, or 10! is,

10! = 10 ⋅ 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 36,28,800

• Value of factorial 11, or 11 factorial, or 11! is,

11! = 11 ⋅ 10 ⋅ 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 3,99,16,800

and so on.

What is the factorial of 100:

The value of factorial of 100, or 100 factorial is calculated, through its definition, this way:

100! = 100 ⋅ 99 ⋅ 98 ⋅ … ⋅ 3 ⋅ 2 ⋅ 1

=93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000

The approximate value of 100! is 9.3326215443944e+157.

In 100!, the number of trailing zeros is 24.

In 100!, the number of digits is 158.

Properties of factorial:

• n! = n · (n−1) · (n−2) · … · 3 · 2 · 1

• 0! = 1! = 1

• n! = n · (n−1)! = n · (n−1) · (n−2)!

• n! / r! = n · (n−1) … (r+1)

• Factorials of negative numbers and fractions are not defined.

• The definition of the factorial function can be extended to non-negative arguments using the gamma function, where,

Γ(n+1) = n!

Why factorial is important in mathematics:

Generally, factorial was given a lot of attention throughout the whole history of mathematics, which is totally fair. The factorial function is probably one of the most famous functions in mathematics, notably in combinatorics, algebra, and mathematical analysis.

The factorial is important in mathematics because it represents the number of ways we can arrange things. For example, consider a bookshelf with 12 magazines. How many different ways do you think you could arrange those? The correct answer to this question is 12! and we know that 12! = 479001600, so there are 479001600 ways to arrange the 12 magazines.

As the above example shows, the factorial function grows very quickly! In fact, it grows at a super-exponential rate. That is, it grows more rapidly than exponentially.

(Source – Various books from the college library)

Tags: what is 100 factorial, what is the factorial of hundred, n factorial, n factorial formula, what is n factorial

Copyrighted Material © 2019 - 2024 Prinsli.com - All rights reserved

All content on this website is copyrighted. It is prohibited to copy, publish or distribute the content and images of this website through any website, book, newspaper, software, videos, YouTube Channel or any other medium without written permission. You are not authorized to alter, obscure or remove any proprietary information, copyright or logo from this Website in any way. If any of these rules are violated, it will be strongly protested and legal action will be taken.