Correlation in Hindi

सहसंबंध (Correlation):

दो सांख्यिकीय चरों के बीच सम्बन्ध का माप सहसम्बन्ध (Correlation) कहलाता है। इससे पता चलता है कि दो चर आपस में कितने सम्बन्धित हैं। दो समंक-श्रेणियाँ सह-सम्बन्धित कही जाती है यदि एक समंक माला (श्रेणी) के चर-मूल्य में परिवर्तन होने पर दूसरी समंक माला (श्रेणी) के चर-मूल्य में भी परिवर्तन होता है। यह कारणता से अलग है।

सहसंबंध एक सांख्यिकीय तकनीक है जो दो या दो से अधिक विचलनों (variables) के बीच संबंधों का अध्ययन करती है। जबकि सहसंबंध विश्लेषण (correlation analysis) में, दो विचलनों के बीच संबंधों की सीमा को मापने के लिए और उसका अध्ययन करने के लिए, उपयोग की जाने वाली विभिन्न विधियों (तरीकों) और तकनीकों को शामिल किया जाता है।

अर्थात्, विचलनों के बीच के संबंध को सहसंबंध कहा जाता है। दो चर x और y सहसंबंध कहलाते हैं यदि एक चर में परिवर्तन के परिणामस्वरूप दूसरे चर में संगत परिवर्तन होता है।

दूसरे शब्दों में, यदि दो चर x और y इस प्रकार से संबंधित हैं कि एक के मान में परिवर्तन के साथ दूसरे के मान में या तो प्रत्यक्ष परिवर्तन होता है या व्युत्क्रम परिवर्तन होता है, तो इन चरों को सह-संबंध कहा जाता है।अर्थात्, सहसंबद्ध चरों में, एक चर में वृद्धि दूसरे चर में वृद्धि या कमी के साथ होती है।

उदाहरण के लिए, किसी वस्तु की कीमत और मांग के बीच सह-संबंध होता है क्योंकि अन्य चीजों को समान रखते हुए, किसी वस्तु की कीमत में वृद्धि से उस वस्तु की मांग में कमी आ जाती है। इसी तरह, छात्रों की ऊंचाई और वजन में, किसी शहर की बरसात में और उस शहर में रेनकोट की बिक्री के बीच में, इन सभी में सह-संबंध होता है।

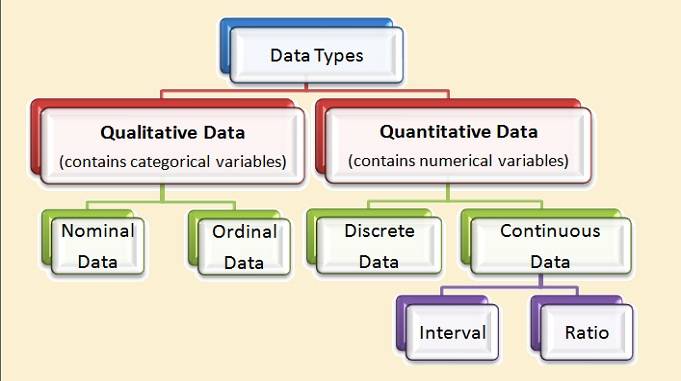
इसलिए, सह-संबंध मात्रात्मक चर और श्रेणीबद्ध चर के बीच संबंधों की जांच के लिए एक सांख्यिकीय पद्धति है। इसे दूसरे तरीके से कहें तो यह इस बात का माप है कि चीजें किस तरह से संबंधित हैं।

सहसंबंध गुणांक (Coefficient of Correlation in hindi):

सह-संबंध के माप को सह-संबंध का गुणांक कहा जाता है (इसे r द्वारा दर्शाते हैं), यह एक ही चित्र में सहसंबंध की दिशा और डिग्री को संक्षेप में प्रस्तुत करता है। दूसरे शब्दों में, सहसम्बन्ध गुणांक दो चरों के परस्पर सम्बन्धों का माप होता है। सहसंबंध गुणांक ज्ञात करने के लिए, दोनों चरों के सहप्रसरण को उनके मानक विचलनों के गुणनफल से भाग देते है। सहसंबंध गुणांक का मान हमेशा -1 और +1 के बीच होता है।

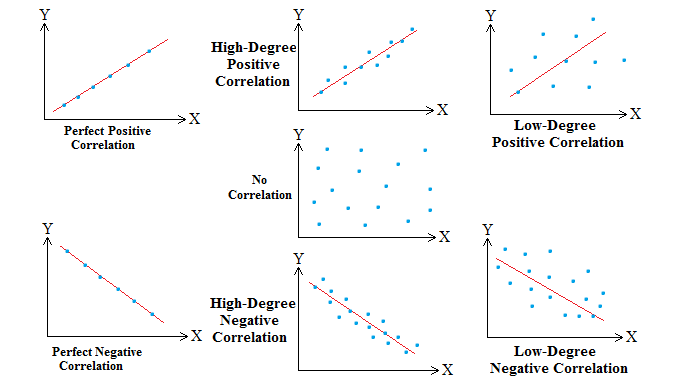
• सहसम्बन्ध गुणांक r का मान +1 होता है, यदि दोनों चरों में पूर्ण सीधा रैखिक सम्बन्ध (perfect direct (increasing) linear relationship) होता है।

• सहसम्बन्ध गुणांक r का मान -1 होता है, यदि दोनों चरों में पूर्ण व्युत्क्रम रैखिक सम्बन्ध (perfect inverse (decreasing) linear relationship) होता है।
• सहसम्बन्ध गुणांक r का मान 0 के निकट होता है, यदि दोनों चरों में बहुत कम सम्बन्ध है।

• अन्य स्थितियों में सहसम्बन्ध गुणांक r का मान -1 और +1 के बीच होता है।

सहसंबंध विश्लेषण (Correlation Analysis in hindi):

सहसंबंध विश्लेषण इस बात का अध्ययन है कि चर कैसे सहसंबद्ध होते हैं। नतीजतन, सहसंबंध विश्लेषण चर के बीच संबंधों की निकटता का आकलन करने के लिए उपयोग की जाने वाली तकनीकों को संदर्भित करता है।

अर्थात, सहसंबंध विश्लेषण (correlation analysis) में, दो विचलनों के बीच संबंधों की सीमा को मापने के लिए और उसका अध्ययन करने के लिए, उपयोग की जाने वाली विभिन्न विधियों (तरीकों) और तकनीकों को शामिल किया जाता है।

सहसंबंध की कुछ महत्वपूर्ण परिभाषाएँ (Important definitions of correlation in hindi):

♦ क्रॉक्सटन और काउडेन (Croxton and Cowden) कहते हैं,

“जब संबंध मात्रात्मक (परिमाणात्मक) प्रकृति का होता है, तो संबंध को खोजने, ज्ञात करने, मापने और इसे एक संक्षिप्त सूत्र में व्यक्त करने के लिए उपयुक्त सांख्यिकीय उपकरण को सहसंबंध कहते है”

♦ ए. एम. टटल (A.M. Tuttle) कहते हैं,

“सहसंबंध दो या दो से अधिक चरों (विचलनों) के बीच सहविचरण का विश्लेषण है।”

♦ डब्ल्यू. ए. नीजवेन्गर (W.A. Neiswanger) कहते हैं,

“सहसंबंध विश्लेषण आर्थिक व्यवहार को समझने में योगदान देता है, आलोचनात्मक रूप से महत्वपूर्ण विचलन का पता लगाने में सहायता करता है, जिस पर अन्य विचलन निर्भर करते हैं, किसी अर्थशास्त्री को ऐसे संबंध प्रकट कर सकते हैं जिनके द्वारा गड़बड़ी फैलती है और उसे उन रास्तों का सुझाव देती है जिनके माध्यम से स्थिरता लाने वाली शक्तियां प्रभावी हो सकें।”

♦ एल. आर. कॉनर (L.R. Conner) कहते हैं,

“यदि दो या दो से अधिक राशियां सहानुभूति में इस प्रकार परिवर्तित होती हैं, जिससे एक राशि में होने वाले परिवर्तन के फलस्वरूप दूसरी राशि में भी परिवर्तन होने की प्रवत्ति पाई जाती है तो उन राशियों को उन्हें सहसंबद्ध कहा जाता है।”

(Source – Various books from the college library)

Copyrighted Material © 2019 - 2024 Prinsli.com - All rights reserved

All content on this website is copyrighted. It is prohibited to copy, publish or distribute the content and images of this website through any website, book, newspaper, software, videos, YouTube Channel or any other medium without written permission. You are not authorized to alter, obscure or remove any proprietary information, copyright or logo from this Website in any way. If any of these rules are violated, it will be strongly protested and legal action will be taken.