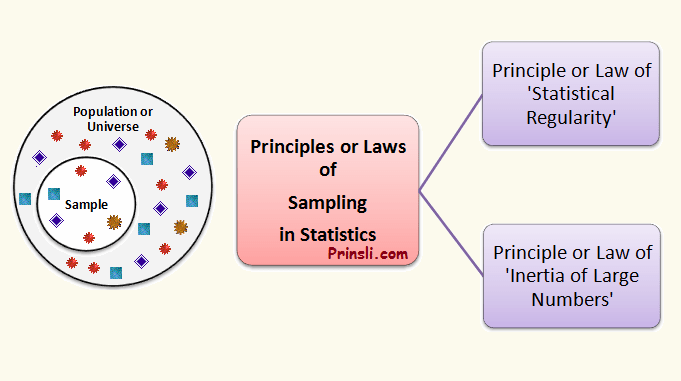
Principles or Laws of Sampling in Statistics:

In Statistics, the theory of sampling is based on two important principles or laws:

(1) Principle or Law of ‘Statistical Regularity’, and

(2) Principle or Law of ‘Inertia of Large Numbers’.

The above principles are two fundamental laws of statistics. When an investigator uses the sampling method in an investigation, these laws are very important.

Read Also: Population, Sample and Sampling in Statistics

In fact, in a sampling investigation, only a few selected items are studied, and the researcher estimates the characteristics of the entire population based on their results. Hence, it is extremely important to choose an adequate sample size and a true representative, so that the sample’s results are as close to those of the population as possible. These statistical laws are based on the sampling technique’s basic requirements.

(1) Principle or Law of ‘Statistical Regularity’:

This principle is derived from the mathematical theory of probability.

This principle states that when a large number of items are selected randomly from the population, the chance is fairly high that these items have the same characteristics as the entire population. In other words, this principle states that if a sample is chosen randomly from a population, it is probable to have almost the same characteristics as that of the population. This principle draws our attention to one very important point: the desirability of selecting the sample randomly.

In the words of Prof. W.I. King,

“The law of statistical regularity lays down that a moderately large number of items chosen at random from a very large group are almost sure on the average to possess the characteristics of the large group.”

In the words of Wheldon,

“The Law of Statistical Regularity states that a reasonably large number of items selected at random from a large group of items will on average, be representative of the characteristics of the large group or population”.

Thus, this principle is defined by the large sample size and the random selection of a representative sample that possesses the characteristics of a large group.

According to this principle, the sample selection is random, that is, every item has an equal and likely chance of being chosen. In other words, the sample must not be chosen deliberately at one’s discretion. It is believed that a sample chosen randomly rather than on purpose serves as a true representative of the population. That is, this type of sample would be representative of the population. If this condition is met, it is possible to depict the characteristics of the population fairly and accurately by studying only a portion of it.

Hence, this principle is extremely useful in practice because it allows for a considerable reduction in the amount of work required before reaching any conclusions about a large population.

In fact, many statistical measures like average, dispersion, correlation, index numbers, etc. are mostly calculated from a sample, and generalisations related to these characteristics can be made correctly if the number of observations (items) is large.

Examples:

(i) If a researcher wants to do a survey on the annual family income of workers in an industry, he cannot collect information on every employee in every firm. Rather, he will select, say, 2000 workers from a total of 50000. If these 2000 workers are chosen randomly and their average annual income is calculated, it will be almost the same as the average income of the entire population.

(ii) Similarly, if a study is to be made about the cigarette buying habits of the students of a University, it is not necessary to study each and every student; instead, a few students may be chosen randomly from each college, and on that basis, conclusions drawn for all university students.

It should be noted that the results obtained from sample data may differ from those obtained from the population. This is due to the fact that the sample is only a subset of the entire population.

This law holds good if the following conditions are met:

(a) The sample, that is, the selection of items from the parent population, is selected randomly.

(b) The sample size, that is, the number of items in the sample is large enough to avoid sampling fluctuation.

(c) Over a long period of time, sampling results will be true on average.

(2) Principle or Law of ‘Inertia of Large Numbers’:

This principle is a corollary of the ‘Statistical Regularity’ principle. It is extremely important in sampling theory.

According to this principle, if all other factors are equal, the larger the sample size, the more accurate the results will be. This is because this principle is based on the concept that large numbers have more stable characteristics than small ones.

When the sample size is large, the variations in the component parts tend to balance each other out, and thus the variation in the aggregate is negligible. This does not imply that there is no variation in larger numbers; there is, but it is less than in small numbers.

Hence, according to the Principle of ‘Inertia of Large Numbers, a larger sample size provides more accurate results, because large numbers are more stable and consistent than small numbers.

Examples:

(i) If a coin is tossed 10 times, we should expect 5 heads and 5 tails. But this experiment has only been tried a few times, it is possible that we will not get exactly 5 heads and 5 tails. The end result could be 9 heads and 1 tail, or 8 heads and 2 tails, or 7 heads and 3 tails, etc. If the same experiment is repeated 10000 times, the chance of getting 5000 heads and 5000 tails is very high, that is, the results will be very close to 50% heads and 50% tails.

The main reason for such probability is that the experiment has been repeated a large enough number of times and the possibility of variations in one direction compensating for others in a different direction is greater. If we get continuously 5 heads at one time, we are likely to get continuously 5 tails at other times, and so on, with the number of heads and tails being more or less equal in the experiment as a whole.

(ii) If we want to study the variation in rice production over a number of years and have collected data from only one or two states of India, the result would show a large variation in production due to favourable or unfavourable factors. On the other hand, if production figures are collected for all of India’s states, we are likely to find little variation in the aggregate. This does not imply that production would remain constant for all years. It simply means that changes in production in individual states will be counterbalanced for the country as a whole.

(iii) It is very unlikely that we will get the correct information if we choose only 2 students from a class of total intelligence level because these two students could be either very intelligent or very poor. But if we select 8, 10, or more students for this purpose, it is quite possible to have a total of 100 students in the sample to learn about students of various levels.

Thus, both principles state that as the sample size increases, the accuracy and reliability of the results will increase proportionally.

(Source – Various books from the college library)

Tags: What are the principles of sampling in statistics? What are the two principles of sampling? What are the important laws on which the theory of sampling is based? What is the meaning of sampling explain principle and importance of sampling? basic principle of sampling, principle of statistical regularity, principles of sampling in research methodology, what are the basic principles on which sampling theory rests? principles of probability sampling, laws of sampling theory, What are the principles of sampling theory?

Copyrighted Material © 2019 - 2024 Prinsli.com - All rights reserved

All content on this website is copyrighted. It is prohibited to copy, publish or distribute the content and images of this website through any website, book, newspaper, software, videos, YouTube Channel or any other medium without written permission. You are not authorized to alter, obscure or remove any proprietary information, copyright or logo from this Website in any way. If any of these rules are violated, it will be strongly protested and legal action will be taken.