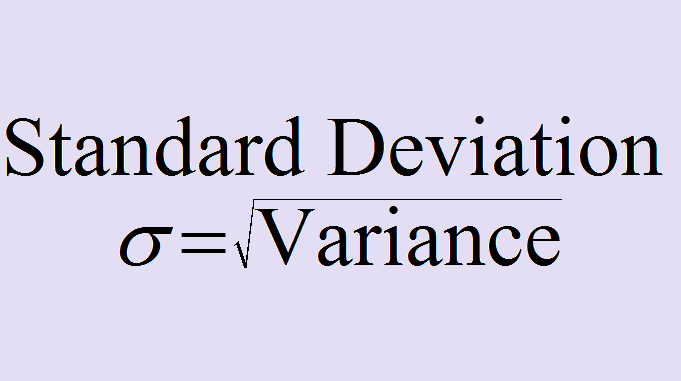
Standard Deviation (S.D.):

The positive square root of the variance is the standard deviation σ. Hence,

Standard Deviation σ = √(Variance)

The standard deviation, denoted by the Greek letter σ (read as sigma), is highly helpful in understanding the mean’s representativeness. While variance gives a rough idea of spread, the standard deviation is more concrete, giving exact distances from the mean. The standard deviation is the basis for determining the proportion of data values within certain distances on either side of the mean for certain types of distributions, so S.D. is a particularly significant measure of distributions.

Karl Pearson established the concept of standard deviation, which has practical value because it is free of all the errors and defects that occur in range, quartile deviation, and average deviation.

The square root of the average of squared deviations taken from the actual mean is used to determine the standard deviation. It’s also referred to as the root mean square deviation. In statistics, variance is defined as the square of standard deviation, or σ².

In terms of raw data, calculation of the standard deviation:

For raw data, there are four methods to calculate standard deviation:

(i) when the actual values ​​are taken;

(ii) when the deviations are taken from the actual mean;

(iii) when the deviations are taken from the assumed mean; and

(iv) When ‘step deviations’ are taken from the assumed mean.

Steps for calculating standard deviation σ :

(i) First calculate the simple mean of the given values or data.

(ii) Then, square the given values ​​and add them.

(iii) Finally, use the formula to get the standard deviation σ.

Some formulas for Standard Deviation are as follows:

• Standard Deviation for Ungrouped Data:

(i) Deviations taken from Actual Mean:

,

where N= Number of the items,

X= The value given in the series, and

Mean of the values.

(ii) Deviations taken from Assumed Mean:

,

where , and A is assumed mean.

• Standard Deviation for Grouped Data:

(i) Deviations taken from Actual Mean:

(ii) Deviations taken from Assumed Mean:

,

where,

• Standard Deviation for first n natural numbers:

• Coefficient of Standard Deviation

• Coefficient of Variation:

C.V.

• Relation between measures of variations:

Q.D. , and

A.D. .

Additional Important Notes for SD:

• The Standard Deviation of the data set 12, 12, 12, 12, 12 is zero (because all values in this data set are the same, that is, the numbers are identical).
• The Standard Deviation cannot be zero unless all values in a data set have the same value (e.g., 12, 12, 12, 12, 12, 12).
• The Standard Deviation remains unchanged if the same number is added to or subtracted from all of the values. For example, the data “34, 65, 45” will have the same standard deviation as data “134, 165, 145”. Because standard deviation depends on the differences between the observations and the mean, and adding 100 to each data value increases the mean also by 100.

(Source – Various books from the college library)

Copyrighted Material © 2019 - 2024 Prinsli.com - All rights reserved

All content on this website is copyrighted. It is prohibited to copy, publish or distribute the content and images of this website through any website, book, newspaper, software, videos, YouTube Channel or any other medium without written permission. You are not authorized to alter, obscure or remove any proprietary information, copyright or logo from this Website in any way. If any of these rules are violated, it will be strongly protested and legal action will be taken.