
What is the Critical Path Method (CPM) in Network Analysis?
CPM was developed in 1957 by M. R. Walker of E. I. Du Pont de Nemours & Co. and J. E. Kelly of Remington Rand to solve the project scheduling problem. It is a method to control cost and time.
CPM is suitable for Non-research projects like civil construction, shipbuilding etc., so it has spread widely and is especially concentrated in the construction and process industries. It employs network analysis to plan production, construction projects, and Research & Development activities. Aside from that, it is used in a variety of other situations that necessitate time and performance estimates.
Critical Path Method (CPM) is one of the basic deterministic network analysis methods. It is Deterministic in nature because different estimates are known in the case of CPM. Its goal is to calculate the project duration using the critical path length, which is a sequence of interdependent activities with the least float.
The amount of time required to complete various parts of the project is assumed to be known with certainty when using CPM. Furthermore, the relationship between the number of resources used and the time required to complete the project is assumed to be known.
The critical path method (CPM) is used for the computation of the earliest and latest time to get the completion day for a project. To compute this, we first find the earliest and latest time for each activity and then calculate the float (slack) and the activity with zero float (slack), this process gives the critical path which constitutes the completion day.
Read Also: Difference between PERT and CPM
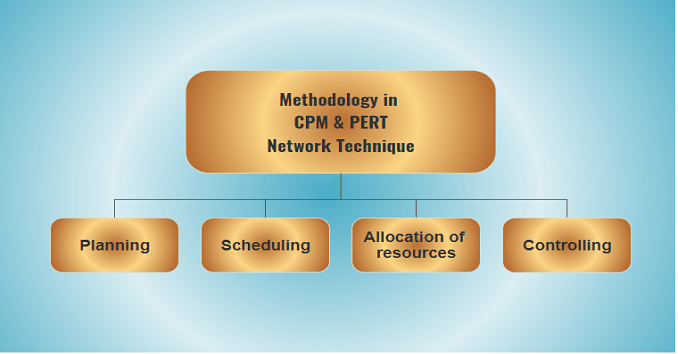
The interactive procedure of determining the critical path involves the following steps:
1. Systematically divide the project into various activities. Label all activities. Arrange all the activities in a logical sequence. Construct the arrow diagram.
2. Number all the nodes (events) and activities. Determine the time for each activity while keeping in mind that it is deterministic. On the arrow diagram, indicate the activity times.
3. Calculate the earliest start time, earliest finish time, latest start time and latest finish time. Make a table for the normal times of activity, as well as the earliest time and latest times.
4. Take the difference between the earliest and latest time for each node to calculate the total float for each activity.
5. Identify the critical activities (the activities with zero float) and connect them to the beginning nodes and ending nodes in the network diagram using a double line arrow. This gives the critical path.
6. Calculate the total project duration.
(Source – Various books of college library)
Copyrighted Material © 2019 - 2024 Prinsli.com - All rights reserved
All content on this website is copyrighted. It is prohibited to copy, publish or distribute the content and images of this website through any website, book, newspaper, software, videos, YouTube Channel or any other medium without written permission. You are not authorized to alter, obscure or remove any proprietary information, copyright or logo from this Website in any way. If any of these rules are violated, it will be strongly protested and legal action will be taken.


The following relates to the activities needed for certain project
Activity Preceded by Time (weeks)
A 15
B 15
C A 3
D A 5
E B,C 8
F B,C 12
G E 1
H E 14
I D,G 3
J F,H,I 14
a. Construct a network diagram (CPA) showing clearly the critical path.
b. What is the shortest possible time (weeks) for completing the jobbing production?
c. If activity B is delayed by two weeks, briefly advise the management on steps they could take to avoid the production taking longer than the shortest possible time obtained in b above.
kindly assist