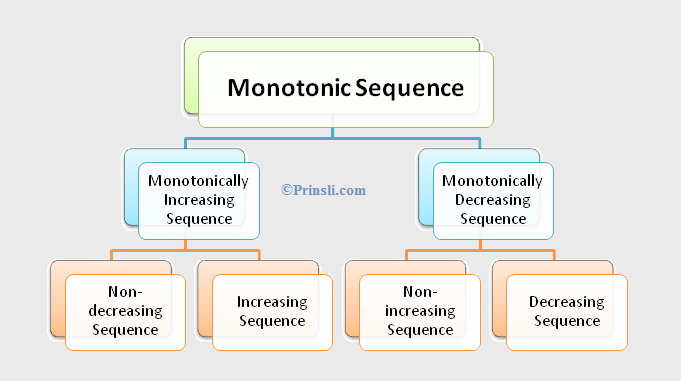
Monotonic Sequence: Definition, Examples, Properties

Lata Agarwal Mathematics & Statistics, Mathpedia, Sequences
monotonic sequence increasing decreasing definition examples properties

Monotonic Sequence Definition:

If a sequence {sn} is either monotonically increasing or monotonically decreasing, then it is said to be monotonic sequence (or monotone sequence).

In other words, a sequence {sn} is said to be a monotonic sequence if it is either increasing (or strictly increasing), non-decreasing, decreasing (or strictly decreasing), or non-increasing.

♦ What is Monotonically Increasing Sequence?

A monotonically increasing sequence {sn} is either an increasing (or strictly increasing) sequence or a non-decreasing sequence.

Increasing Sequence – A sequence {sn} is said to be an increasing or strictly increasing sequence if

{s_n} < {s_{n + 1}} for all n∈N,

that is,

{s_1} < {s_2} < {s_3} < \cdots < {s_n} < {s_{n + 1}} < \cdots

Non-decreasing Sequence – A sequence {sn} is said to be a non-decreasing sequence if

{s_n} \le {s_{n + 1}} for all n∈N,

that is,

{s_1} \le {s_2} \le {s_3} \le \cdots \le {s_n} \le {s_{n + 1}} \le \cdots

For example,

  • The sequence {sn} = {n} = {1, 2, 3, 4, 5, …, n, …} is an increasing or strictly increasing sequence.
  • The sequence {sn} = {2, 2, 4, 4, 6, …} is a non-decreasing sequence.

♦ What is Monotonically Decreasing Sequence?

A monotonically decreasing sequence {sn} is either a decreasing (or strictly decreasing) sequence or a non-increasing sequence.

Decreasing Sequence – A sequence {sn} is said to be decreasing or strictly decreasing sequence if

{s_n} > {s_{n + 1}} for all n∈N,

that is,

{s_1} > {s_2} > {s_3} > \cdots > {s_n} > {s_{n + 1}} > \cdots

Non-increasing Sequence – A sequence {sn} is said to be a non-increasing sequence if

{s_n} \ge {s_{n + 1}} for all n∈N,

that is,

{s_1} \ge {s_2} \ge {s_3} \ge \cdots \ge {s_n} \ge {s_{n + 1}} \ge \cdots

For example,

  • The sequence \{ {s_n}\} = \left\{ {\frac{{n + 1}}{n}} \right\} = \left\{ {2,\frac{3}{2},\frac{4}{3},...} \right\} is a decreasing or strictly decreasing sequence.
  • The sequence {sn} = {6, 5, 5, 4, 3, 3, …} is a non-increasing sequence.

Monotonic Sequence Example:

Determine whether the following sequences are monotonic sequence:

Example 1. \left{ {{s_n}} \right} = \left{ {1,2,3,...,n,...} \right}

This sequence is increasing, so it is a monotonic sequence.

Example 2.

\left\{ {{s_n}} \right\} = \left\{ {\frac{1}{2},\frac{2}{3},\frac{3}{4},...,\frac{n}{{n + 1}},...} \right\}

This sequence is increasing, so it is a monotonic sequence.

Example 3.

\left\{ {{s_n}} \right\} = \left\{ {1,\frac{1}{2},\frac{1}{3},...,\frac{1}{n},...} \right\}

This sequence is decreasing, so it is a monotonic sequence.

Example 4.

\left\{ {{s_n}} \right\} = \left\{ {0,1,0,1,...} \right\}

This sequence is neither increasing nor decreasing, so it is not a monotonic sequence.

Example 5.

\left\{ {{s_n}} \right\} = \left\{ {1, - \frac{1}{2},\frac{1}{5},1,...} \right\}

This sequence is neither increasing nor decreasing, so it is not a monotonic sequence.

Example 6.

\left\{ {{s_n}} \right\} = \left\{ {2, - 2,4, - 4,6, - 6,...} \right\}

This sequence is neither increasing nor decreasing, so it is not a monotonic sequence.

Example 7.

\left\{ {{s_n}} \right\} = \left\{ { - \frac{1}{n}} \right\} = \left\{ { - 1, - \frac{1}{2}, - \frac{1}{3},..., - \frac{1}{n},...} \right\}

This sequence is increasing, so it is a monotonic sequence.

Example 8.

\left\{ {{s_n}} \right\} = \left\{ {\frac{{{2^n}}}{{n!}}} \right\}

This sequence is decreasing, so it is a monotonic sequence.

Important Remark:

  • Every increasing sequence is also non-decreasing, while the opposite is not true. Similarly, Every decreasing sequence is also non-increasing, while the opposite is not true.
  • Unfortunately, some authors mistakenly refer to a non-decreasing sequence as increasing, or a non-increasing sequence as decreasing, which is incorrect in the strict sense.
  • For example, the sequence {1, 1, 2} is not increasing (or strictly increasing), since {s_1} = {s_2} = 1; however, it is non-decreasing because {s_n} \le {s_{n + 1}} for all n.

Properties of Monotonic Sequences:

  • Monotonic sequences are generally easier to handle than sequences that can go both up and down.
  • The convergence problem for a monotonic sequence is relatively simple.

We can imagine an increasing sequence increasing indefinitely and diverging to +∞, or it increasing up to a certain limit. The third option is not possible.

Similarly, we might see a decreasing sequence decreasing till it reaches a limit, or we can imagine it decreasing indefinitely and diverging to −∞. The third option is not possible.

  • Monotonic sequences either converge or diverge, they cannot oscillate. The fact that monotonic sequences cannot oscillate is what makes them so important.

Read Also: Sequence Definition

Copyrighted Material © 2019 - 2024 Prinsli.com - All rights reserved

All content on this website is copyrighted. It is prohibited to copy, publish or distribute the content and images of this website through any website, book, newspaper, software, videos, YouTube Channel or any other medium without written permission. You are not authorized to alter, obscure or remove any proprietary information, copyright or logo from this Website in any way. If any of these rules are violated, it will be strongly protested and legal action will be taken.

About Lata Agarwal 270 Articles
M.Phil in Mathematics, skilled in MS Office, MathType, Ti-83, Internet, etc., and Teaching with strong education professional. Passionate teacher and loves math. Worked as a Assistant Professor for BBA, BCA, BSC(CS & IT), BE, etc. Also, experienced SME (Mathematics) with a demonstrated history of working in the internet industry. Provide the well explained detailed solutions in step-by-step format for different branches of US mathematics textbooks.
Website Facebook LinkedIn

Related Articles

definition of sequence in math
Sequences

Definition of Sequence in Mathematics

Lata Agarwal Sequences

A sequence in a set S is a rule which assigns to each natural number a unique element of S. A sequence whose range is a subset of R is called a real sequence or a sequence of real numbers. […]

definition of sequence in math
Sequences

Basic Operations on Sequences

Lata Agarwal Sequences

We know that the operations of addition, subtraction, multiplication, and division can all be defined using real numbers. These operations can easily be applied to a set of sequences. […]

Sequence in hindi
Mathpedia

Sequence in hindi – अनुक्रम: परिचय, परिभाषा, निरूपण, उदाहरण

Lata Agarwal Mathpedia, Sequences

Sequence in hindi: अनुक्रम: परिचय, परिभाषा, निरूपण, उदाहरण, वास्तविक संख्याओं के अनुक्रम (Sequences of Real Numbers)… […]

Be the first to comment

Leave a Reply

Your email address will not be published.


*