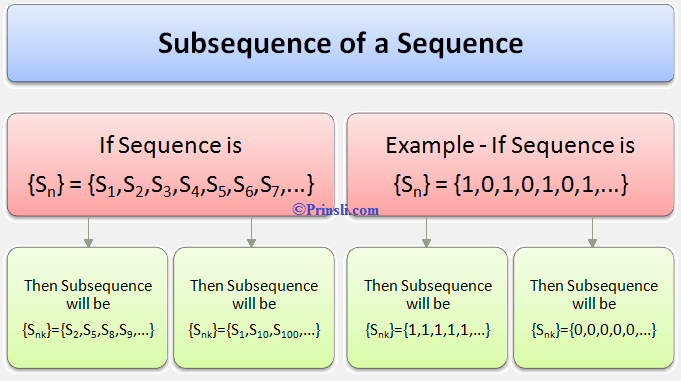
Introduction of Subsequence of a Sequence in Mathematics-
Consider the following sequence:
This sequence appears to include the two sequences {1, 2, 3, …} and {−1,−2,−3,…} within itself. To have a word to express this, we use the term ‘subsequence’. Thus, we can say that the last two sequences are subsequences of the first.
We can say that a subsequence in mathematics, is obtained by removing some of the original sequence’s terms. That is, a subsequence of a given sequence is a sequence that can be obtained from the given sequence by deleting some or no elements while keeping the order of the remaining elements unchanged. In other words, an infinitely ordered subset of a sequence is called a subsequence.
For example, for a sequence {}, the subsequences are,
{}, {
} etc.
Often, the best way to study a sequence is to look at some of its subsequences.
Mathematical Definition of Subsequence of a Sequence:
Consider the following sequence:
Then the following sequence,
,
where is strictly increasing sequence of natural numbers (that is,
), is called a subsequence of this {
}.
NOTE:
The condition: ; states that the order of the various terms in the subsequence is the same as it is in the sequence.
For Example:
Consider the following:
This sequence {} is a subsequence of the following sequence,
because {} contains just the 1st, 3rd, 5th, etc. terms of the original sequence {
}. In this case,
.
Examples of Subsequence:
Example 1.
Consider the following sequence:
that is, .
(i) If we take , then {
} is a sequence of natural number such that
.
Hence,
is a subsequence of {}.
(ii) Similarly, if we take , then {
} is a sequence of natural number such that
.
Hence,
is a subsequence of {}.
Example 2.
The sequence of primes {} is a subsequence of the sequence of positive integers {
}.
Example 3.
The sequence of squares of primes {} is not a subsequence of the sequence of positive integers {
}. Because, in this case,
, and {
} or {
} is not a strictly increasing sequence of natural numbers.
Subsequence Theorem:
- If a sequence {
} converges to a limit l, then any subsequence {
} of {
} also converges to the limit l.
- All subsequences of a convergent sequence converge to the same limit.
- Bolzano-Weierstrass Theorem states that “Every bounded sequence in Rn has a convergent subsequence.”
- Every sequence is a subsequence of itself.
- Every subsequence of a subsequence of a given sequence is itself a subsequence of the given sequence.
Copyrighted Material © 2019 - 2024 Prinsli.com - All rights reserved
All content on this website is copyrighted. It is prohibited to copy, publish or distribute the content and images of this website through any website, book, newspaper, software, videos, YouTube Channel or any other medium without written permission. You are not authorized to alter, obscure or remove any proprietary information, copyright or logo from this Website in any way. If any of these rules are violated, it will be strongly protested and legal action will be taken.



This information helps me very much thanks u